Q-learning is an algorithm, that contains many of the basic structures required for reinforcement learning and acts as the basis for many more sophisticated algorithms. The Q-learning algorithm can be seen as an (asynchronous) implementation of the Robbins-Monro procedure for finding fixed points. For this reason we will require results from Robbins-Monro when proving convergence.
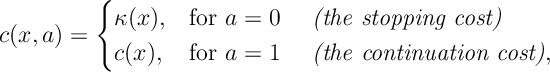
![V(x) = \maxi_{\Pi \in {\mathcal P} } \quad R(x,\Pi) := \mathbb{E}_{x_0} \left[ \sum_{t=0}^{\infty} \beta^{t} r(X_t,\pi_t) \right] \, .](https://appliedprobability.blog/wp-content/uploads/2019/01/c0c1e66eb9b0cb64c2860e22d53a5d16.png?w=840)