We want to optimize the expected value of some random function. This is the problem we solved with Stochastic Gradient Descent. However, we assume that we no longer have access to unbiased estimate of the gradient. We only can obtain estimates of the function itself. In this case we can apply the Kiefer-Wolfowitz procedure.
The idea here is to replace the random gradient estimate used in stochastic gradient descent with a finite difference. If the increments used for these finite differences are sufficiently small, then over time convergence can be achieved. The approximation error for the finite difference has some impact on the rate of convergence.
Continue reading “Zero-Order Stochastic Optimization: Keifer-Wolfowitz”
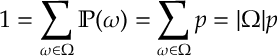 (where
(where 