Probability and Set Operations

(This is a section in the notes here.)

We want to calculate probabilities for different events. Events are sets of outcomes, and we recall that there are various ways of combining sets. The current section is a bit abstract but will become more useful for concrete calculations later.

Operations on Events.

Definition [Union] For events $A,B \subseteq \Omega$ , the union of $A$ and $B$ is the set of outcomes that are in $A$ or $B$ . The union is written $\begin{aligned} A \cup B \, .\end{aligned}$ We can say “ $A$ or $B$ ” as well as “ $A$ union $B$ ”.

Definition [Intersection] For events $A,B \subseteq \Omega$ , the intersections of $A$ and $B$ is the set of outcomes that are in both $A$ and $B$ . The union is written $\begin{aligned} A \cap B \, .\end{aligned}$ We can say “ $A$ and $B$ ” as well as “ $A$ intersection $B$ ”.

Definition [Complement] For event $A \subseteq \Omega$ , the complement of $A$ is the set of outcomes in the sample space $\Omega$ that are not in $A$ . We denote the complement of $A$ with¹ $\begin{aligned} A^c \, .\end{aligned}$ We can say “not $A$ ”.

Definition [Relative Complement] For events $A,B \subseteq \Omega$ , the relative complement of $B$ relative to $A$ is the set of outcomes not in $B$ that are in $A$ . The relative complement of $B$ relative to $AA$ is written $\begin{aligned} A \backslash B\, .\end{aligned}$ We can say “A not B”.

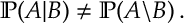
Warning! Later we will define $\mathbb P ( A | B)$ to denote the probability of $A$ given $B$ . The line $"|"$ in $\mathbb P ( A | B)$ is straight and whereas line $"\backslash"$ in $A \backslash B$ in the relative complement is not a straight. So be warned that, in general, $\begin{aligned} \mathbb P(A | B) \neq \mathbb P (A \backslash B)\, .\end{aligned}$

Here are a few facts about sets

Lemma 1. For events $A,B,C \subseteq \Omega$
i) $\begin{aligned} A \cap B = B \cap A, \quad A \cup B = B \cup A, \quad (A^c)^c = A \,.\end{aligned}$ ii) $\begin{aligned} A \cup (B \cup C) = (A \cup B) \cup C\;\,\\ A \cap (B \cap C) = (A \cap B )\cap C \,.\end{aligned}$ iii) $\begin{aligned} A \cap ( B \cup C) = (A \cap B) \cup (A \cap C) \,\,\\ A \cup ( B \cap C) = (A \cup B) \cap (A \cup C) \, .\end{aligned}$ iv) (De Morgan’s Laws) $\begin{aligned} (A \cup B )^c = A^c \cap B^c\,\,\\ (A \cap B )^c = A^c \cup B^c\, .\end{aligned}$ v) If $A \subseteq B$ then $B^c \subseteq A^c$ .
vi) $A \backslash B = A \cap B^c$ .

Remarks.
$\bullet$ The proof of each statement above is quite straightforward. For each statement, we can draw a Venn diagram (i.e. we draw 1,2, or 3 intersecting circles and shade the appropriate areas to check the result.) For instance, the first statement in Lemma 1iii) can be seen in Figure 1, below.

Figure 1. A Venn Diagram verifying that $A \cap ( B \cup C) = (A \cap B) \cup (A \cap C)$

$\bullet$ From i) and ii) we see that it does not matter what order we apply unions and intersections. For that reason, when we apply a sequence of unions or a sequence of intersections we can unambiguously write $\begin{aligned} \bigcup_{i=1}^\infty A_i \qquad \text{and} \qquad \bigcap_{n=1}^\infty A_n \, .\end{aligned}$

$\bullet$ The statement iii) is analogous to the statement that $a \times (b+c) = a \times b + a \times c$ .

$\bullet$ In De Morgan’s Laws, iv), we can think of the complement of union being intersection. I.e. $\cup^c = \cap$ and $\cap^c = \cup$ . ² Thus $\begin{aligned} (A\cup B)^c = A^c \cup^c B^c = A^c \cap B^c\, .\end{aligned}$

Probability Rules for Operations on Sets

We can now start to think about what these operations on events imply for the probabilities of those events. Here are a sequence of lemma to this effect. (You can skip the proofs on first reading.)

Lemma 2. If $A$ and $B$ have not outcome in common, i.e. $A \cap B = \emptyset$ , then³ $\begin{aligned} \mathbb P (A \cup B ) = \mathbb P (A) + \mathbb P(B) \, .\end{aligned}$

Proof.

$\mathbb P (A \cup B) = \sum_{\omega \in A \cup B } \mathbb P(\omega) =\sum_{\omega \in A } \mathbb P(\omega) +\sum_{\omega \in B } \mathbb P(\omega) = \mathbb P(A) + \mathbb P(B) \, .$

Lemma 2 can be extended to a countable set of sets $A_1,A_2,...$ with $A_n \cap A_m = \emptyset$ . So $\begin{aligned} \mathbb P \Bigg( \bigcup_{n=1}^\infty A_n \Bigg) = \sum_{n=1}^\infty \mathbb P ( A_n ) \, .\end{aligned}$ The above equality is actually an axiom of probability. $\square$

Lemma 3. If $A \subseteq B$ then $\mathbb P(A) \leq \mathbb P(B)$

Proof. Using Lemma 1ii) and v), $B = (A \cap B) \cup (A^c \cap B)= A \cup (B \backslash A) \, .$ Using Lemma 2 and the fact probabilities are non-negative $\begin{aligned} \mathbb P( B) = \mathbb P(A) + \mathbb P( B \backslash A) \geq \mathbb P(A) \, .\end{aligned}$

$\square$

Suppose I have a statement like “I have a red car” this implies “I have a car”. So the probability “I have a car” is more than the probability “I have a red car”. The above shows that this inequality holds for any two statements where one implies the other.

Lemma 4. $\mathbb P (A \cup B) = \mathbb P(A) + \mathbb P(B) - \mathbb P(A\cap B) \,.$

(An intuitive proof of this lemma: draw a Venn diagram with events $A$ and $B$ . Notice if we colour in $A$ and then colour in $B$ then we end up colouring $B\cap A$ twice. So if we want to count that region once, which we do for the event $A \cup B$ , we need to subtract $B\cap A$ once.)

Proof. Note that $\begin{aligned} \label{eq:op3-1} \mathbb P (A \cup B ) = \mathbb P (A \backslash B ) + \mathbb P(B\backslash A) + \mathbb P (A \cap B)\end{aligned}$ where as $\begin{aligned} \mathbb P (A )+\mathbb P (B ) =& [ \mathbb P (A \backslash B ) +\mathbb P (A \cap B)] + [\mathbb P(B\backslash A) + \mathbb P (A \cap B)] \notag \\ = & \mathbb P (A \backslash B ) + \mathbb P (B \backslash A ) + 2 \mathbb P(A \cap B) \, .\label{eq:op3-2}\end{aligned}$ Subtracting from gives $\begin{aligned} \mathbb P (A )+\mathbb P (B ) - \mathbb P (A\cup B) = \mathbb P( A \cap B) \,.\end{aligned}$ Rearranging the above expression gives the result. $\square$

It is often easy to calculate $\mathbb P(A \cap B)$ from $\mathbb P(A)$ and $\mathbb P(B)$ (see later discussion on independence). The above lemma gives a way to access $\mathbb P(A\cup B)$ from $\mathbb P(A \cap B)$ .

Lemma 5. $\begin{aligned} \mathbb P (A) = 1 - \mathbb P( A^c) \, .\end{aligned}$

Proof. $A \cup A^c = \Omega$ while $A \cap A^c = \emptyset$ . Also $\mathbb P (\Omega ) = 1$ since probabilities sum to one (see Definition [probdef]). So $\begin{aligned} 1 = \mathbb P(\Omega) = \mathbb P ( A \cup A^c ) = \mathbb P(A) + \mathbb P(A^c) \, .\end{aligned}$ Rearranging gives the required result. $\square$

Sometimes the number of outcomes in $A$ is large. So we may need to sum the probability of a lot of different outcomes to get $\mathbb P(A)$ . However, it may be that $A^c$ only has a few outcomes. So it may be simple to calculate $\mathbb P(A^c)$ . The above lemma then gives us a way to get $\mathbb P(A)$ .

Other notations exist for the complement such as $\bar A$ .↩
This is not a mathematically precise statement but is useful for remembering the rule.↩
Here recall that $\emptyset$ is the empty set, which is the set containing no outcomes.↩