What follows is a heuristic derivation of the Stochastic Integral, Stochastic Differential Equations and Itô’s Formula.
Continuous Time Dynamic Programming
Discrete time Dynamic Programming was given in the post Dynamic Programming. We now consider the continuous time analogue.
Optimal Stopping
An Optimal Stopping Problem is an Markov Decision Process where there are two actions: 
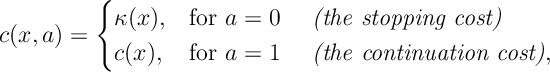
This defines a stopping problem.
Algorithms for MDPs
For infinite time MDPs, we cannot apply to induction on Bellman’s equation from some initial state – like we could for finite time MDP. So we need some algorithms to solve MDPs.
Markov Chains: A Quick Review
This section is intended as a brief introductory recap of Markov chains. A much fuller explanation and introduction is provided in standard texts e.g. Norris, Bremaud, or Levin & Peres (see references below).
Infinite Time Horizon
Thus far we have considered finite time Markov decision processes. We now want to solve MDPs of the form 
Markov Decision Processes
Markov decision processes are essentially the randomized equivalent of a dynamic program.
Dynamic Programming
We briefly explain the principles behind dynamic programming and then give its definition.
Notes for Stochastic Control 2019
The link below contains notes PDF for this years stochastic control course
I’ll upload individual posts for each section. I’ll likely update these notes and add more exercises over the coming semester. I’ll add this update in a further post at the end of the course. Comments, typos, suggestions are always welcome.
Applied Probability Notes 