Finance for Actuarial

A summary of Finance for Actuarial course:

  • Cash Flows; Time & Rounding Conventions; Glossary of (some) Financial Products
  • Simple & compound interest; Rate of Discount; Nominal Interest; Accumulation Factors; Force of Interest
  • Discounted, Accumulate & Present Value; Continuous Cash flows.
  • Annuties Immediate & Due; present and future values; increasing & perpetuities…
  •  Loan schedules; Level Installments; APR and Flat rate
  • Equations of Value and Yield.

(This covers about half of the Institute and Faculty of Actuaries CT1 exam — though you should probably work on context if you want to pass the exam.)

Continue reading “Finance for Actuarial”

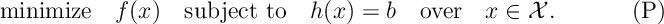
Talagrand’s Concentration Inequality

We prove a powerful inequality which provides very tight gaussian tail bounds “e^{-ct^2}” for probabilities on product state spaces \Omega^n. Talagrand’s Inequality has found lots of applications in probability and combinatorial optimization and, if one can apply it, it generally outperforms inequalities like Azzuma-Hoeffding.

Continue reading “Talagrand’s Concentration Inequality”

Lecture 0. Some Basic Maths for Actuarial Students

We will regularly need to employ certain calculations. In MATH10951 the context might vary but the maths varies much less. These notes are more of a background check on prequisties. We cover

  • Power, the exponential, logarithms, the (natural) logarithm.
  • Arithmetic and Geometric progressions.

Continue reading “Lecture 0. Some Basic Maths for Actuarial Students”