Q-learning

Q-learning is an algorithm, that contains many of the basic structures required for reinforcement learning and acts as the basis for many more sophisticated algorithms. The Q-learning algorithm can be seen as an (asynchronous) implementation of the Robbins-Monro procedure for finding fixed points. For this reason we will require results from Robbins-Monro when proving convergence.

A key ingredient is the notion of a $Q$ -factor as described in Section [IDP]. Recall that optimal $Q$ -factor, $Q(x,a)$ , is the value of starting in state $x$ taking action $a$ and thereafter following the optimal policy. In Infinite Time Horizon, Prop 2 we showed that this solved the recursion:

$\label{QL:FixedPoint} Q(x,a) = \mathbb E_{x,a} [ r(x,a) + \beta \max_{\hat{a}} Q(\hat{X},\hat{a}) )]\, .$

Def. [Q-learning] Given a state $x$ , an action $a$ , its reward $r(x,a)$ and the next state $\hat{x}$ , $Q$ -learning performs the update

$Q(x,a) \xleftarrow[]{\alpha} r(x,a) + \beta \max_{a'\in \mathcal A} Q(\hat{x},a') - Q(x,a)$

where $\alpha$ positive (learning rate) parameter. Recall $x \xleftarrow[]{\alpha} dx$ means reset $x$ with $x'$ such that $x' = x + \alpha dx$ .

To implement this as an algorithm, we assume that we have a sequence of state-action-reward-next_state quadruplets $\{ (x_t,a_t,r_t,\hat{x}_t) \}_{t=0}^\infty$ and we apply the above update to each of the terms in this sequence.

Thrm 1. For a sequence of state-action-reward triples $\{ (x_t,a_t,r_t,\hat{x}_t) \}_{t=0}^\infty$ Consider the Q-learning update for $(x,a,r,\hat{x}) = (x_t,a_t,r_t,\hat{x}_t)$

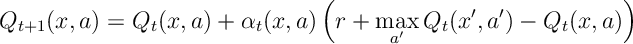
$Q_{t+1}(x,a) = Q_t(x,a) + \alpha_t ( x,a) \left( r + \max_{a'} Q_t(x',a') - Q_t(x,a) \right)$

if the sequence of state-action-reward triples visits each state and action infinitely often, and if the learning rate $\alpha_t(x,a)$ is an adapted sequence satisfying the Robbins-Monro condition

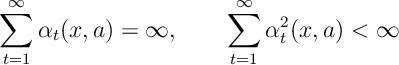
$\sum_{t=1}^\infty \alpha_t(x,a) = \infty , \qquad \sum_{t=1}^\infty \alpha^2_t(x,a) < \infty$

then, with probability $1$ ,

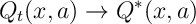
$Q_t(x,a) \rightarrow Q^*(x,a)$

where $Q^*(x,a)$ is the optimal value function.

Proof. We essentially show that the result is a consequence of Theorem 3 in Robbins-Monro. We note that the optimal $Q$ -function, $\mathbf Q = (Q(x,a) : x\in \mathcal X, a\in \mathcal A)$ satisfies a fixed point equation

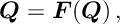
$\bm Q = \bm F(\bm Q)\, ,$

with

for each $x\in \mathcal X$ and $a\in \mathcal A$ . We know from Prop 2 in the post Infinite Time Horizon, that for discounted programming $\mathbf F (\cdot)$ is a contraction. I.e.

$|| \bm F ( \bm Q_1 ) - \bm F ( \bm Q_2) ||_{\infty} \leq \beta || \bm Q_1 - \bm Q_2 ||_{\infty} \, .$

Now notice that the $Q$ -learning algorithm performs the update

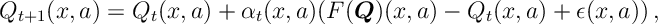
$Q_{t+1}({x,a}) =Q_t(x,a) + \alpha_t(x,a) ( F(\bm Q)(x,a) - Q_t(x,a) + \epsilon(x,a)) \, ,$

where $\epsilon(x,a) = r + \beta \max_{\hat{a}} Q(\hat{X},\hat{a}) - \mathbb E_{x,a} [ r(x,a) + \beta \max_{\hat{a}} Q(\hat{X},\hat{a}) ]$

for $(x_t,a_t,r_t,\hat x_t )=(x,a,r,\hat{x})$ . The update above is a Robbin’s Monro update. Further Notice $Q(x',a')$ remains the same for all other values of $x,a$ , the update is asynchronous. It is not hard to see that when we condition on $\mathcal F_t$ the set of previous actions and states that

$\mathbb E [\epsilon_t(x_t,a_t) | \mathcal F_t] = 0$

and, a quick calculation shows,¹ that

$\mathbb E [\epsilon_t(x_t,a_t)^2 | \mathcal F_t] \leq 2 r^2_{\max} + 2 \beta^2 \max_{x,a} Q_t(x,a)^2 \, .$

From this we see that we are working in the setting of Theorem 3 in Robbins-Monro and that the conditions of that theorem are satisfied. Thus it must be that

$Q_t(x,a) \xrightarrow[t\rightarrow\infty ]{} Q^*(x,a)$

where $Q^*(x,a)$ satisfies $\mathbf Q^* = \mathbf F(\mathbf Q^*)$ . In otherwords, as required, it satisfies the Bellman equation for the optimal $Q$ -function and thus is optimal. $\square$

Literature.

The argument here is depends heavily on the fixed point results. But the main source used is

Tsitsiklis, John N. “Asynchronous stochastic approximation and Q-learning.” Machine learning 16.3 (1994): 185-202.

Note $(x+y)^2 \leq 2 x^2+2 y^2$ ↩

Share this:

Leave a comment Cancel reply