We briefly describe an Online Bayesian Framework which is sometimes referred to as Assumed Density Filer (ADF). And we review a heuristic proof of its convergence in the Gaussian case.
Bayes Rule gives
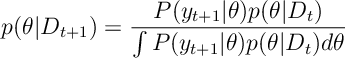
For data , parameter
and new data point
.
ADF suggests projecting data at time to a parameter (vector)
. This gives a routine that consists of the following two steps. (See [Opper] for the main reference article)
Update:
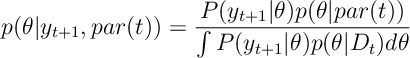
Project:
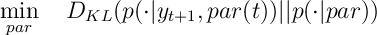
Here is the KL-divergence of distributions
and
Remark. Note that for exponential families of distributions:
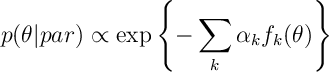
then matching moments of gives the minimization of the above.
Let’s assumes that is a normally distributed with mean
and covariance matrix
.
Under this one can argue that obeys the recursion
(1)
![\label{Opper:1} \hat \theta_i (t+1) - \hat \theta_i (t) = \sum_j C_{ij}(t) \partial_j \log \mathbb E_u [ P(y_{t+1} | \hat \theta (t) + u ) ]](https://appliedprobability.blog/wp-content/uploads/2019/03/6d83e4472b9baca5561a65f447df671a.png?w=840)
and obeys the recursion:
(2)
![\label{Opper:2} C_{ij}(t+1) = C_{ij}(t) + \sum_{kl} C_{ik}(t) C_{lj}(t) \partial_k \partial_l \log \mathbb E_u [P(y_{t+1} | \hat \theta (t) + u) ]\, .](https://appliedprobability.blog/wp-content/uploads/2019/03/50cc513ca17a33c1d4ae6ac37bc9c571.png?w=840)
Here is normal with mean zero and covariance
. The partial derivative,
, above is taken with respect to the
th component of
.
Quick Justification of (1) and (2)
Note that
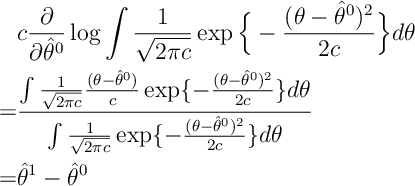
A similar calculation gives the other expression on .
For
![V_{kl} = \partial_k \partial_l \log \mathbb E_u [P(y_{t+1} | \hat \theta (t) + u) ]](https://appliedprobability.blog/wp-content/uploads/2019/03/e12e0748090610a1f863091009f1faf7.png?w=840)
This gives the differential equation
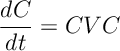
This implies
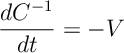
because
![]()
We assumes is drawn IID from a distribution
. We assumes there is an attractive fixed point
satisfying
(3)
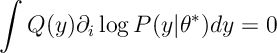
So
![\begin{aligned} \lim_{t\rightarrow\infty} \frac{C^{-1}(t)}{t} & = \lim_{t\rightarrow\infty} \frac{1}{t} \int^t_0 V(s) ds \\ &= \mathbb E_Q [ \partial_k \partial_l \log \mathbb E_u [P(y_{t+1} | \theta^* + u) ] ] \\ &\approx \mathbb E_Q [ \partial_k \partial_l \log \mathbb E_u [P(y_{t+1} | \theta^* ) ] ] = J(\theta^*)\end{aligned}](https://appliedprobability.blog/wp-content/uploads/2019/03/4e894b5c1538cb3948cd2795e5db8bde.png?w=840)
The last approximation that removes the normal distribution error needs justifying. The inequality with assumes that
(in the case where they are not equal – i.e. when the model is miss specified – we just puts in some matrix
instead of
)
In principle should not be too far from
, because
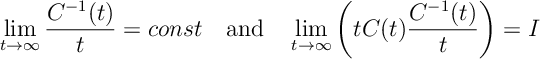
imply that
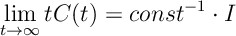
so the variance of
goes to zero at rate
justifying the approximation for
. From the above we see that “const” is
(or
if the
)). So
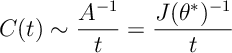
Next we start to analyse the error:
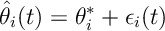
He notes that by and then a Taylor expansion that

Next we see that using
![\frac{ d e_i }{ dt } = \frac{ e_i }{t} + \sum_j \frac{ J^{-1} }{ t } \mathbb E_Q [\partial_j \log P]\, .](https://appliedprobability.blog/wp-content/uploads/2019/03/e6cebbee7a77ce38b8b1c996e3d18a8b.png?w=840)
The sum on the right-hand side goes to zero because of . So we get

It is also possible to analyze
. The above expressions give

(again using ) which is solved by
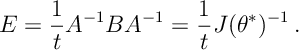
This is actually the same convergence as expected by MLE estimates.
Literature
This is based on reading Opper and Winther:
Opper, Manfred, and Ole Winther. “A Bayesian approach to on-line learning.” On-line learning in neural networks (1998): 363-378.