Markov Decision Processes

Markov Decisions Problems; Bellman’s Equation; Two examples

A Markov Decision Process is a Dynamic Program where the state evolves in a random/Markovian way.

As in the post on Dynamic Programming, we consider discrete times $t=0,1,...,T$ , states $x\in\mathcal{X}$ , actions $a\in\mathcal{A}_t$ and rewards $r_t(a_t,x_t)$ . However, the plant equation and definition of a policy are slightly different.

Def 1 [Plant Equation] The state evolves according to functions $f_t: \mathcal{X}\times \mathcal{A}_t \times [0,1] \rightarrow \mathcal{X}$ . Here

$x_{t+1} = f_t(x_t,a_t; U_t) \equiv f_t(x_t,a_t)$

where $(U_t)_{t\geq 0}$ are IIDRVs uniform on $[0,1]$ . This is called the Plant Equation. As noted in the equivalence above, we will often suppress dependence on $U_t$ . Also, we will use the notation

$\mathbb{E}_{x_t a_t} [G({x}_{t+1})] = \mathbb{E} [G(f_t(x_t,a_t))]$

Def 2 [Policy] A policy $\pi$ choses an action $\pi_t$ at each time $t$ as a function of past states $x_0,...,x_t$ and past actions $\pi_0,...,\pi_{t-1}$ . We let $\mathcal{P}$ be the set of policies.

A policy, a plant equation, and the resulting sequence of states and rewards describe a Markov Decision Process. Objective is to find a process that optimizes the following objective.

Def 3 [Markov Decision Problem] Given initial state $x_0$ , a Markov Decision Problem is the following optimization

$\begin{aligned} W(x_0) =& \text{Maximize} \quad R_T(x_0,\Pi):= \mathbb{E} \left[ \sum_{t=0}^{T-1} r_t(x_t,\pi_t) + r_T(x_T)\right]\\ &\text{over} \qquad\qquad \Pi \in \mathcal{P}.\notag \end{aligned}$

Further, let $R_\tau({x_\tau, \Pi})$ (Resp. $W_\tau(x_\tau)$ ) be the objective (Resp. optimal objective) for when the summation is started from time $t=\tau$ and state $x_\tau$ , rather than $t=0$ and $x_0$ .

Ex 1 [the Bellman Equation]Setting $W_T(x)=r_T(x)$ for $t=T-1,T-2,...,0$

$\tag{Bell eq.} W_t(x_t) = \sup_{a_t\in\mathcal{A}_t} \left\{ r_t(x_t,a_t) + \mathbb{E}_{x_t,a_t} \left[ W_{t+1}(x_{t+1})\right] \right\}.$

The above equation is Bellman’s equation for a Markov Decision Process.

Ex 2 You need to sell a car. At every time $t=0,...,T-1$ , you set a price $p_t$ and a customer then views the car. The probability that the customer buys a car at price $p$ is $D(p)$ . If the car isn’t sold be time $T$ then it is sold for fixed price $W_T$ , $W_T<1$ . Maximize the reward from selling the car and find the recursion for the optimal reward when $D(p) = (1-p)_+$ .

Ex 3 You own a call option with strike price $p$ . Here you can buy a share at price $p$ making profit $x_t-p$ where $x_t$ is the price of the share at time $t$ . The share must be exercised by time $T$ . The price of stock $x_t$ satisfies $x_{t+1} = x_t + \epsilon_t$ for $\epsilon_t$ IIDRV with finite expectation. Show that there exists a decreasing sequence $\{a_t\}_{0\leq t \leq T}$ such that it is optimal to exercise whenever $x_s \geq a_s$ occurs.

Answers

Ans 1 $\mathcal{P}_t$ , the set policies that can be implemented from time $t$ to $T$ , is the product actions at time $t$ and the set of policies from time $t+1$ onward. That is $\mathcal{P}_t = \{ (\pi_t,\Pi): \Pi \in\mathcal{P}_{t+1}, \pi_t: \mathcal{X}^t \times \prod_{\tau = 0}^{t-1}\mathcal{A}_\tau \rightarrow \mathcal{A}_t \}$ .

$\begin{aligned} W_t(x_t) &= \sup_{\Pi_t \in \mathcal{P}_t} \mathbb{E}_{x_t \pi_t} \left[ \sum_{t=0}^{T-1} r_t(x_t,\pi_t) + r_T(x_T)\right]\\ &= \sup_{\pi_t } \sup_{\Pi \in \mathcal{P}_{t+1}} \Bigg\{ r_t(x_t,\pi_t) + \mathbb{E}_{x_t \pi_t} \Bigg[\mathbb{E}_{x_{t+1} \pi_{t+1}}\Bigg[\sum_{\tau=t+1}^{T-1} r_{\tau}(x_\tau,\pi_\tau) + r_T(x_T)\Bigg]\Bigg]\Bigg\}\\ &= \sup_{a\in\mathcal{A} } \Bigg\{ r_t(x_t,a) + \mathbb{E}_{x_t\, a} \Bigg[ \underbrace{\sup_{\Pi \in \mathcal{P}_{t+1}}\mathbb{E}_{x_{t+1} \pi_{t+1}}\Bigg[\sum_{\tau=t+1}^{T-1} r_{\tau}(x_\tau,\pi_\tau) + r_T(x_T)\Bigg]}_{=W_{t+1}(x_{t+1})}\Bigg]\Bigg\} \end{aligned}$

2nd equality uses structure of $\mathcal{P}_t$ , takes the $r_t$ term out and then takes conditional expectations. 3rd equality takes the supremum over $\mathcal{P}_{t+1}$ , which does not depend on $\pi_t$ , inside the expectation and notes the supremum over $\pi_t$ is optimized at a fixed action $a\in\mathcal{A}$ (i.e. the past information did not help us.)

Ans 2 The optimal reward from time $t$ onward (assuming you still have the car) satisfies:

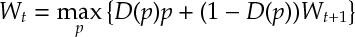
$W_{t} = \max_p \left\{ D(p)p +(1-D(p)) W_{t+1}\right\}$

If $D(p)=(1-p)_+$ then $W_t= (1+W_{t+1})^2/4$ . (Note the relation is monotone and $W_0$ converges to fixed point if $T\rightarrow \infty$ .)

Ans 3 Taking the and subtracting $x$ gives

$\label{MDP:BellCall} W_t(x)-x = \max\left\{ -p, \mathbb{E}\left[W_{t+1}(x+\epsilon_t) -x \right] \right\}$

1) $W_t(x)\geq W_{t+1}(x)$ , because all policies implemented from time $t+1$ are subset of policies from time $t$ .

2) $W_t(x)-x$ is decreasing and cts in $x$ because $W_T(x)= \max \{x-p, 0\}$ is and, since expectation and maximum preserve these properties, so is $W_t$ by induction on .