We consider one of the simplest iterative procedures for solving the (unconstrainted) optimization

$\label{GD:Opt} \text{minimize}\qquad f(x) \qquad\text{over}\qquad x\in{\mathbb R}^p$

where $f$ is a convex function twice differentiable function. For fixed $x,v\in{\mathbb R}^p$

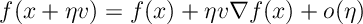
$f(x+\eta v) = f(x) + \eta v \nabla f(x) +o(\eta)$

If $||v||=1$ , the gradient is most negative when $v\propto -\nabla f(x)$ . Thus, starting from $x_0$ define the gradient descent algorithm:

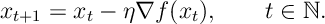
$x_{t+1}=x_t - \eta\nabla f(x_t) , \qquad t\in{\mathbb N}.$

We assume $H(x)$ the Hessian matrix of $f$ at $x$ satisfies $b ||v||^2\leq \frac{1}{2} v^T H(x)v\leq B ||v||^2$ , for some $b,B>0$ .So, by a Taylor expansion $\label{GD:hess} f(x_{t+1}) -f(x_t) \leq - \eta ||\nabla f(x_t)||^2 + B\eta^2 ||\nabla f(x_t)||^2,$
$v\in{\mathbb R}^p$
We assume $0< \eta < B^{-1}$ . So the right-hand inequality above guarantees that $f(x_{t+1})<f(x_t)$ for all $t$ .
We assume there is a unique finite solution to our optimization.¹

We now see our algorithm converges exponentially fast to its solution, so-called linear convergence.

Given the assumptions above there exists $\kappa\in (0,1)$ and $K>0$ such that

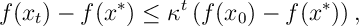
$f(x_{t}) - f(x^*) \leq \kappa^t \left( f(x_{0}) - f(x^*) \right),$

$\label{GD:x} || x_t- x^* || \leq \kappa^t K$

Rewriting , we have $f(x_{t+1}) - f(x^*) \leq f(x_t) - f(x^*) - \eta (1- B\eta) ||\nabla f(x_t)||^2$

Using lower bound on the Hessian, we bound $||\nabla f(x_t)||^2$ with the following Taylor expansion

$\begin{aligned} f(x^*)-f(x_t) &\geq & (x^*-x_t) \cdot \nabla f(x_t) + b || x^*-x_t||^2 \\ &\geq & \min_{x'}\left\{ x'\cdot \nabla f(x_t) + b || x'||^2\right\}=-\frac{1}{4b}|| \nabla f(x_t)||^2 \end{aligned}$ C

ombining the last two inequalities, we have as required,

$f(x_{t+1}) - f(x^*) \leq \underbrace{(1- 4b\eta (1-B \eta))}_{=\kappa} \Big[ f(x_{t}) - f(x^*) \Big].$

Finally for , we reapply our Hessian lower-bound assumption and use the above bound for $f(x_{t}) - f(x^*)$ :

$\begin{aligned} b|| x_t-x^* ||^2 & \leq & (x_t-x^*) \nabla f(x^*) + b|| x_t-x^* ||^2 \\ & \leq & f(x_t)-f(x^*) \\ &\leq &\kappa_1^t (f(x_0)-f(x^*)). \end{aligned}$

Projected Gradient Descent

We consider a simple iterative procedure for solving a constrained optimization

$\label{GD:Opt} \text{minimize}\qquad f(x) \qquad\text{over}\qquad x\in {\mathcal X}$

where $f$ is a convex function twice differentiable function and where ${\mathcal X}\subset {\mathbb R}^p$ is some non-empty closed convex set, eg. $\{ x \geq 0 : Ax = b\}$ . Like in Section [GD]we want to follow the steepest descent direction $x_{t+1}=x_t - \eta\nabla f(x_t)$ . However, such points need not belong to ${\mathcal X}$ . Thus we consider the projection of $x\in{\mathbb R}^p$ on to ${\mathcal X}$ :

$P_{{\mathcal X}}(x)= \argmin_{y\in {\mathcal X}} || x - y ||^2$

and then, from $x_0$ , we define the projected gradient descent by

$x_{t+1}= P_{{\mathcal X}} ( x_t - \eta_t\nabla f(x_t) ), \qquad t\in{\mathbb N}$

After projecting it need not be true that $f(x_{t+1})<f(x_t)$ . Thus we adjusted the step-size $\eta_t>0$ and our proof will study the distance between $x_t$ and the optimal solution $x^*$ rather than the gap $f(x_t)-f(x^*)$ .

• The key observation is that making a projection cannot increase distances

[PGD:proj] $||P_{\mathcal X}(x)-P_{\mathcal X}(y)|| \leq ||x-y||$

For all $x'\in {\mathcal X}$ , we must have $(x'- P_{\mathcal X}(x))\cdot (x-P_{\mathcal X}(x)) \leq 0$ , i.e. the plane ${\mathcal H}= \{z: (z- P_{\mathcal X}(x))\cdot (x-P_{\mathcal X}(x))=0\}$ separates $x$ from ${\mathcal X}$ . If this were not true, then we would have a contradiction, in particular, there would be a point on the line joining $x'$ and $P_{\mathcal X}(x)$ that is closer to $x$ . We thus have

$(P_{\mathcal X}(y)- P_{\mathcal X}(x))\cdot (x-P_{\mathcal X}(x)) \leq 0\quad$ $(P_{\mathcal X}(x)- P_{\mathcal X}(y))\cdot (y-P_{\mathcal X}(y)) \leq 0.$

Adding together and then applying Cauchy-Schwartz implies

$\begin{aligned} & &||P_{\mathcal X}(y)- P_{\mathcal X}(x))||^2 \\ &\leq & (y-x)\cdot (P_{\mathcal X}(y)-P_{\mathcal X}(x)) \\ &\leq & ||y- x|| \; ||P_{\mathcal X}(y)- P_{\mathcal X}(x))||,\end{aligned}$

as required.

If the gradient of iterates are bounded, $K=\max_{t\in{\mathbb N}}\{||\nabla f(x_t)||^2 \} < \infty$ then

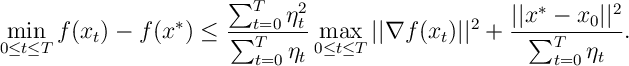
$\min_{0\leq t \leq T} f(x_t) -f(x^*) \leq \frac{\sum_{t=0}^T \eta^2_t}{\sum_{t=0}^T \eta_t} \max_{0\leq t \leq T} ||\nabla f(x_t)||^2+ \frac{||x^*-x_0||^2}{ \sum_{t=0}^T \eta_t} .$

Hence if $\sum_{t=0}^\infty \eta_t =\infty$ , $\sum_{t=0}^\infty \eta_t^2 <\infty$ and $\max_{0\leq t \leq T} ||\nabla f(x_t)||^2<\infty$ then $\lim_{T\rightarrow\infty} f(x^*) - \min_{0\leq t \leq T} f(x_t)=0$ .

$\begin{aligned} & & || x_{t+1} - x^* ||^2 \\ &= & || P_{\mathcal X} (x_t-\eta_t \nabla f(x_t) ) -x^* ||^2 \\ &\underbrace{\leq}_{\text{by Lemma }\ref{PGD:proj}} & || x_t-x^*-\eta_t \nabla f(x_t ) ||^2 \\ &= & || x_t-x^*||^2 + \eta_t \underbrace { \nabla f(x_t) \left(x^*-x_t\right)}_{\substack{\leq f(x^*)-f(x_t),\\\text{ by convexity}}} + \eta_t^2 || \nabla f(x_t)||^2\\ & \leq & || x_t-x^*||^2 + \eta_t\left( f(x^*)-f(x_t)\right) + \eta_t^2 || \nabla f(x_t) ||^2\end{aligned}$

Recurring the above expression yields $\begin{aligned} 0&\leq &|| x_{T+1} - x^* ||^2 \\ &\leq & || x_0-x^*||^2 + \sum_{t=0}^T \eta_t\left( f(x^*)-f(x_t)\right) + \sum_{t=0}^T \eta_t^2 || \nabla f(x_t) ||^2\\ & \leq & || x_0-x^*||^2 + \left( f(x^*)-\min_{0\leq t\leq T} f(x_t)\right) \sum_{t=0}^T \eta_t +\max_{0\leq t \leq T} || \nabla f(x_t) ||^2 \sum_{t=0}^T \eta_t^2 . \end{aligned}$ Rearranging the above gives the required result.

This assumption is not really needed, but it saves space.↩

Projected Gradient Descent

Share this:

Leave a comment Cancel reply