Sums and Limits of Coin Throws

We explain why certain distributions arise naturally as the limit of coin throws.

Bernoulli, Binomial Distributions, Geometric Distributions.
Binomial to Poisson Distribution; Geometric to Exponential; Binomial to Normal.

Bernoulli random variables are just choice tosses: heads or tails; zero or one random variables. You can get surprisingly far – perhaps almost everywhere – in probability by summing and limiting sequences of these random variables.

Def [Bernoulli Random Variable] A random variable $X$ that takes at most two values is called a Bernoulli random variable. We assume (unless stated otherwise) that these values are zero or one. So

${\mathbb P} (X=1)=p, \qquad \text{or} \qquad {\mathbb P} (X=0)=1-p.$

for some $p\in [0,1]$ . We write $X\sim Bern(p)$

Ex 1 [Bernoulli to Binomial] Let $X_i$ , $i=1,...n$ be IID Bernoulli RVs, let

$Y = \sum_{i=1}^n X_i.$

Show that

${\mathbb P} (Y=k) = { n \choose k } p^k (1-p)^{n-k}.$

Ans 1 Probability of $k$ ones in a row and $n-k$ zeros in a row is $p^k (1-p)^{n-k}$ . The number of sequence with $k$ ones and $n-k$ zeros is

${ n \choose k }.$

Def [Binomial Distribution] A RV $Y$ has a Binomial distribution, and we write $Y\sim Bin(n,p)$ when

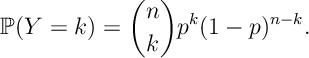
${\mathbb P} (Y=k) = { n \choose k } p^k (1-p)^{n-k}.$

Ex 2 [Bernoulli to Geometric] Consider a sequence of Bernoulli RVs $X_1,X_2,...$ . Let $G$ be the index of the first $1$ in this sequence. Show that

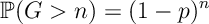
${\mathbb P} ( G > n) = (1-p)^n$

Ans 2

${\mathbb P} (G > n) = {\mathbb P} (X_1=...=X_n=0) = (1-p)^n$

Def [Geometric Distribution] A RV $G$ has Geometric Distribution, and we write $G \sim Geom(p)$ if

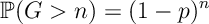
${\mathbb P} ( G > n) = (1-p)^n$

We now consider some limits of Binomial Random Variables.

Ex 3 [Binomial to Poisson]Consider a sequence of Binomial RVS: $Y^n\sim Bin (n, \frac{\lambda}{n})$ for some $\lambda >0$ . Show that

${\mathbb P} ( Y^n = k) \xrightarrow[n\rightarrow\infty]{} e^{-\lambda} \frac{\lambda^k}{k!}$

Ans 3

$\begin{aligned} {\mathbb P} ( Y^n = k ) & = { n \choose k } \left( \frac{\lambda}{n} \right)^k \left( 1- \frac{\lambda}{n} \right)^{n-k} \\ & = \left[ \frac{n}{n} \cdot \frac{n-1}{n} \cdot ... \cdot \frac{n-k+1}{n} \cdot \left( 1-\frac{\lambda}{n} \right)^{-k} \right] \left( 1-\frac{\lambda}{n} \right)^n \frac{\lambda^k}{k!} \\ & \xrightarrow[n\rightarrow\infty]{} e^{-\lambda} \frac{\lambda^k}{k!}\end{aligned}$

Above the term in square brackets goes to one and $(1-\lambda/n)^n$ goes to $e^{-\lambda}$ .

Def [Poisson Distribution] For parameter $\lambda>0$ , a RV $N$ Poisson distribution and we write $N\sim Po(\lambda)$ if

${\mathbb P} (N=k) = e^{-\lambda} \frac{\lambda^k}{k!}.$

Ex 4 [Geometric to Exponential] Consider a sequence of Geometric RVS: $X^n\sim Geom (\frac{\lambda}{n})$ for some $\lambda >0$ . Show that

${\mathbb P} \left(\frac{X^n}{n} > x\right) \xrightarrow[n\rightarrow \infty]{} e^{-\lambda x}$

Ans 4

${\mathbb P} \left( X^n > nx \right) = \left( 1- \frac{\lambda}{n} \right)^{\lfloor nx\rfloor } \xrightarrow[n\rightarrow\infty]{} e^{-\lambda x}.$

We now work to show that the sum of binomial distributions converges to a specific distribution called the normal distribution.

Thrm [Binomial to Normal] If $Y \sim Bin (2n , \frac{1}{2})$ then

$\mathbb{P} \left( a \leq \frac{ Y - \mathbb{E} Y }{ \sqrt{var(Y) 2n} } \leq b \right) \xrightarrow[n\rightarrow \infty]{} \int_{a}^{b} \frac{1}{\sqrt{2\pi}} e^{ - \frac{x^2}{2} } dx$

Def [Normal Distribution] For mean $\mu$ and variance $\sigma^2$ we say that $Z$ has a normal distribution and write $Z\sim {\mathcal N}(\mu,\sigma^2)$ when

$\mathbb{P} \left( a \leq Z \leq b \right) = \int_{a}^{b} \frac{1}{\sqrt{2\pi}} e^{ - \frac{x^2}{2} } dx$

This is a special case of the central limit theorem, and involves several steps.

Ex 5 [Binominal to Normal] If $Y \sim Bin (2n , \frac{1}{2})$ Show that

$\mathbb{P} \left( Y = n + k \right) = \mathbb{P} \left( Y = n \right) \cdot \frac{ \Big( 1- \frac{1}{n}\Big) \Big( 1- \frac{2}{n}\Big) ... \Big( 1- \frac{(k-1)}{n}\Big) }{ \Big( 1+ \frac{1}{n}\Big) \Big( 1+ \frac{2}{n}\Big) ... \Big( 1+ \frac{(k-1)}{n}\Big) }$

Ans 6

$\frac{ \mathbb{P} \left( Y = n + k \right) }{ \mathbb{P} \left( Y = n \right) } = \frac{ { 2n \choose n+k } \frac{1}{2^{2n}} }{ { 2n \choose n } \frac{1}{2^{2n}} } = \frac{ n!n! }{ (n-k)! (n+k)! }$

Cancelling and dividing by $n^k$ gives the required result.

Ex 7 [Continued] Show that

$\frac{ \Big( 1- \frac{1}{n}\Big) \Big( 1- \frac{2}{n}\Big) ... \Big( 1- \frac{(k-1)}{n}\Big) }{ \Big( 1+ \frac{1}{n}\Big) \Big( 1+ \frac{2}{n}\Big) ... \Big( 1+ \frac{(k-1)}{n}\Big) } = \exp \Big\{ -\frac{k^2}{n} + O\Big(\frac{k^4}{n^2} \Big) \Big\}.$

Ans 7 Applying the approximation $\left( 1-x \right)= e^{-x +O(x^2)}$ we have that

$\Big( 1- \frac{1}{n}\Big) \Big( 1- \frac{2}{n}\Big) ... \Big( 1- \frac{(k-1)}{n}\Big) = \exp \left\{ - \frac{1}{n}\sum_{\kappa=1}^{k-1} k \right\} = \exp \Big\{ -\frac{k^2}{2n} + O\Big(\frac{k^4}{n^2} \Big) \Big\}.$

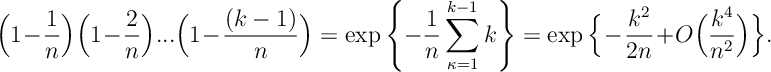
Applying this also to the denominator gives the result.

Ex 8 Show, using Stirling’s Approximiation, that, as $n\rightarrow \infty$ ,

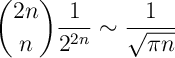
${ 2n \choose n } \frac{1}{2^{2n}} \sim \frac{1}{\sqrt{\pi n}}$

Ans 8 By Stirlings, $latex n! \sim \sqrt{2\pi n}\cdot e^{-n} n^n$,

${ 2n \choose n } \frac{1}{2^{2n}} \sim \frac{ 2\sqrt{\pi n} e^{-2n} 2^{2n} n^{2n} }{ 2\pi n e^{-2n} 2^n n^{2n} } =\frac{1}{\pi n}$

Ex 9 [Continued] Argue that Thrm [SL:Bin2Norm] holds i.e. that

$\mathbb{P} \left( a \leq \frac{ Y - \mathbb{E} Y }{ \sqrt{var(Y) 2n} } \leq b \right) \xrightarrow[n\rightarrow \infty]{} \int_{a}^{b} \frac{1}{\sqrt{2\pi}} e^{ - \frac{x^2}{2} } dx$

Ans 9 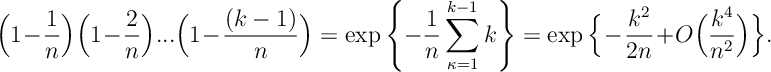In our case the probability corresponds to the sum

$\begin{aligned} &\sum_{n } \mathbb{I}\Bigg[a\sqrt{\frac{n}{2}} \leq Y-n \leq b \sqrt{\frac{n}{2}} \Bigg] \mathbb{P} \left( Y = n + k \right) \\ = & \sum_{n } \mathbb{I}\Bigg[a\sqrt{\frac{n}{2}} \leq k \leq b \sqrt{\frac{n}{2}} \Bigg] \frac{1}{\sqrt{\pi n}}\exp \Big\{ -\frac{k^2}{n} + O\Big(\frac{k^4}{n^2} \Big) \Big\} \\ \approx & \int_{a\sqrt{\frac{n}{2}}}^{b\sqrt{\frac{n}{2}}} \frac{1}{\sqrt{n\pi}} \exp \Big\{ -\frac{k^2}{n} \Big\} dk \\ = & \int_{a}^{b} \frac{1}{\sqrt{2\pi}} \exp \Big\{ -\frac{x^2}{2} \Big\} dk\end{aligned}$