Entropy and Boltzmann’s Distribution

Entropy and Relative Entropy occur sufficiently often in these notes to justify a (somewhat) self-contained section. We cover the discrete case which is the most intuitive.

Entropy – Discrete Case

Def 1. [Entropy] Suppose that $X$ is a random variable with values in the countable set ${\mathcal X}$ and distribution $P=(p_i:i\in {\mathcal X})$ then

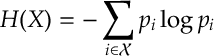
$H(X) = -\sum_{i\in {\mathcal X}} p_i \log p_i$

is the entropy of $X$ .

Def 1. [Relative Entropy] For probability distributions $latex {\mathbb P}=(p_i:i\in {\mathcal X})$ and ${\mathbb Q}=(q_i:i\in {\mathcal X})$ then

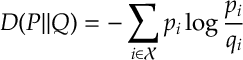
$D(P||Q) = -\sum_{i\in {\mathcal X}} p_i \log \frac{p_i}{q_i}$

is the Relative Entropy of $P$ with respect to $Q$ .

Ex 1. For a vector ${\mathbf n}=(n_i : i=1,...,m)$ with $latex n=\sum_in_i$ , if

then

$\lim_{n\rightarrow \infty} \frac{1}{n} \log\left( \begin{array}{c} n \\ n_i\: : \: i=1,...,m \end{array} \right) = -\sum_{i=1}^m q_i \log q_i$

Ans 1. Take logs and apply the Stirling’s approximation that $\log(n!)=n\log n - n + o(n)$ . So,

$\begin{aligned} \log \left( \begin{array}{c} n \\ n_i\: : \: i=1,...,m \end{array} \right) & =n\log n - n -\sum_{i=1}^m (n_i\log n_i -n_i) + o(n) \\ &=n\log n - \sum_{i=1}^m np_i \log p_i -\sum_{i=1}^\infty np_i\log n + o(n) \\ &=-n\sum_{i=1}^m p_i\log p_i +o(n).\end{aligned}$

Ex 2. Suppose that $X_k$ , $k=1,...,n$ are IIDRVs with distribution $P$ . Let $\hat{P}^n=(\hat{P}_i^n : i \in {\mathcal X} )$ be the in empirical distribution of $X_k$ , $k=1,..,n$ , that is

$\hat{P}^{n}_{i} = \frac{1}{n} \sum_{k=1}^{n} {\mathbb I}[X_k=i]$

If $n_i/n \rightarrow q_i$ for each $i=1,...,m$ then

$\lim_{n\rightarrow \infty} \frac{1}{n} \log \mathbb{P} \left( \hat{P}_n = \frac{ \mathbf{n} }{ n } \right) = - D(Q||P)$

Ans 2. Note that $p_i^{n_i} = e^{nq_i \log p_i}$ , so combining with [1] gives

$\lim_{n\rightarrow \infty} \frac{1}{n} \log \mathbb{P} \left( \hat{P}_n = \frac{ \mathbf{n} }{ n } \right) = -H(Q) + \sum_{i} q_i \log p_i = -D(Q||P).$

Boltzmann’s distribution

We now use entropy to derive Boltzmann’s distribution.

Consider a large number particles. Each particle can take energy levels $e_i$ , $i\in {\mathbb N}$ . Let $\bar{e}$ be the average energy of the particles. If we let $p_i$ be the proportion of particles of energy level $e_i$ then these constraints are

$\sum_{i=1}^\infty p_i =1 \quad\text{and}\quad \sum_{i=1}^\infty e_ip_i=\bar{e}.$

As is often considered in physics, we assume that the equilibrium state of the particles is the state $p$ with the largest number of ways of occurring subject to the constraints on the system. In other words, We solve the optimization

$\begin{aligned} \label{Ent:BoltzOpt} \text{maximize} \quad -\sum_{i=1}^\infty p_i \log p_i \quad &\text{subject to} \quad \sum_{i=1}^\infty p_i=1,\quad \sum_{i=1}^\infty e_ip_i = \bar{e}\\ & \text{over} \quad p_i\geq 0,\;\; \forall i\in\bN. \notag\end{aligned}$

Ex 3. [Boltzmann’s distribution] Show that the solution to is given by the distribution

$p_i=\frac{e^{-\lambda e_i}}{Z(\lambda)}$

is called Boltzmann’s distribution. The scaling constant $Z(\lambda)$ is called the Partition function and the constant $\lambda$ is chosen so that

$\bar{e} = -\frac{\partial{\log Z(\lambda)}}{\partial \lambda}.$

Ans 3. The Lagrangian of this optimization problem is

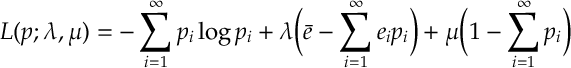
$L(p;\lambda, \mu) =-\sum_{i=1}^\infty p_i\log p_i + \lambda \bigg(\bar{e} - \sum_{i=1}^\infty e_ip_i \bigg) + \mu \bigg( 1- \sum_{i=1}^\infty p_i \bigg)$

So, finding a stationary point

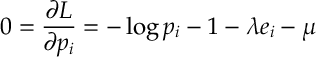
$0=\frac{\partial L}{\partial p_i}=-\log p_i -1 -\lambda e_i -\mu$

which implies

$p_i = \frac{ e^{-\lambda e_i}}{e^{1+\mu}}=\frac{e^{-\lambda e_i}}{Z} \quad\text{where we define} \quad Z=e^{1+\mu}.$

For our constraints to be satisfied, we require that

$1=\sum_{i=1}^\infty p_i\quad \implies \quad Z=\sum_{i=1}^\infty e^{-\lambda e_i},\quad\text{and}\quad \bar{e}=\sum_{i=1}^\infty e_i p_i \quad \implies \quad \bar{e} = \sum_{i=1}^\infty e_i \frac{e^{-\lambda e_i}}{Z}.$

Thinking of $Z$ as a function of $\lambda$ , we call $Z(\lambda)=\sum_{i=1}^\infty e^{-\lambda e_i}$ the partition function and notice it is easily shown that