Cross Entropy Method

In the Cross Entropy Method, we wish to estimate the likelihood

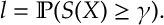
$l = {\mathbb P} ( S(X) \geq \gamma ).$

Here $X$ is a random variable whose distribution is known and belongs to a parametrized family of densities $f( , v)$ . Further $S(X)$ is often a solution to an optimization problem.

It is assumed that $l$ is a relatively rare event, say of order $10^{-5}$ . One way to estimate $l$ is to take $N$ IID samples $X_1,...,X_N$ and then average

$\hat{l} = \frac{1}{N} \sum_{i=1}^N {\mathbb I} [S(X_i) \geq \gamma ].$

This gives us an unbiased estimate. However, because the event is rare, we may require a large number of samples $N$ in order to provide a good estimate of $l$ . Importance sampling is a straightforward method that can mitigate these effects. Here sample each $X_i$ from a different density $g(\cdot)$ and perform the estimate

$\label{CEM:Importance} \hat{l}_g = \frac{1}{N} \sum_{i=1}^N {\mathbb I} [S(X_i) \geq \gamma ] W(x)$

where W(x) = f(x)/g(x). Such a change can improve the estimation of $l$ . For instance, the choice $g^*(x)= {\mathbb I} [ S(x) \geq \gamma ] f(x)/l$ gives the correct estimate of $l$ with certainty. Clearly $g^*$ cannot work in practice; it requires knowledge of $l$ , the parameter which we are estimating. Nonetheless a good estimate of $g^*$ may be possible. The point of the cross entropy method is to find a reasonable choice for $g$ so that importance sampling can be applied.

In particular, the cross-entropy method advocates estimating $g^*(\cdot)$ by $f(\cdot ; v)$ according to a parameter choice that minimizes the relative entropy between $g^*$ and $f(\cdot, v)$ . Namely,

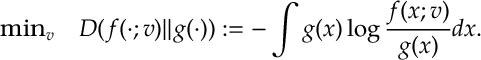
$\text{min}_{v}\quad D( f(\cdot ; v) || g(\cdot) ) := - \int g(x) \log \frac{f(x; v)}{g(x)} dx.$

With a little rearrangement, we see that this is equivalent to the optimization

$\max_v \quad \int {\mathbb I} [S(x) \geq \gamma ] f(x;u) \log f(x; v) dx.$

With importance sampling in mind, we apply a change of measure to the above integral to get

$\max_v \quad \int {\mathbb I} [S(x) \geq \gamma ] f(x;w) W(x;u,v) \log f(x; v) dx$

where $W(x; u,w)=f(x;u)/f(x;w)$ . The above optimization may not be explicitly solvable so we replace it with the (importance sampled) optimization

$\label{CEM:Max} \max_v \frac{1}{N} \sum_{i=1}^N {\mathbb I} [S(X_i) \geq \gamma ] W(X_i ; u,w) \log f(x;v) dx$

where $X_i$ are IID samples from density $f(\cdot ; w)$ .

In many examples the above optimization in concave and solvable either by descent methods or by differentiating and solving for the condition

$\sum_{i=1}^N {\mathbb I} [S(X_i) \geq \gamma ] W(X_i ; u,w) \nabla \log f(x;v) = 0.$

The reason for incorporating importance sampling into the estimate is because the event $\{ \}$ could be too unlikely to form an accurate estimate under the choice $w=v$ . The idea behind the cross entropy method is to apply a multi-level approach where we sequentially increase $\gamma$ and $w$ as follows

We estimate the $\rho$ -th percentile of $S(X)$ by taking by ordering the samples $S(X_1)\leq S(X_2) \leq ... \leq S(X_N)$ and calculating the empirical $\rho$ -th percentile, which gives the update

$\gamma' = S_{\lceil (1-\rho) N \rceil}$

The event $\rho$ is chosen to be reasonably likely, e.g. $\rho = 0.01$ . Note that since, in principle, the parameter $\gamma'$ is such that less likely $\{ S(X) \geq \gamma' \}$ under $v$ when compared with the previous choice of $\gamma$ .

Given this $\gamma'$ , we find $v'$ as the best estimate according to our cross-entropy rule . This, in principle, should increase the likelihood of the event $\{ S(X) \geq \gamma' \}$ when compared with prior choice of $v$ .
When $\gamma'$ passes the required target level $\gamma$ then the have found a parameter choice that gives reasonable importance to the event $\{ S(X) \geq \gamma\}$ and we can calculate $l$ with importance sampling rule .