Blackwell Approachability

Sequentially a player decides to play $\{p_t\}_{t=1}^\infty$ and his adversary decides $\{q_t\}_{t=1}^\infty$ . At time $t$ , a decision $(p_t,q_t)$ results in a vector payoff $A(p_t,q_t)\in {\mathbb R}^k$ . Given $a_t$ is the average vector payoff at time $t$ , Blackwell’s Approachability Theorem is a necessary and sufficient condition so that, regardless of the adversary’s decisions, the player makes the sequence of vectors $\{a_t\}_{t=1}^\infty$ approach a convex set ${\mathcal A}$ .

We consider a sequence $(p_1,q_1), (p_2,q_2), (p_3,q_3), ...$ . Here each $p_t$ is a probability distribution on a set of (pure) decisions $\{1,...,n\}$ and similarly $q_t$ is a probability distribution on $\{1,...,n\}$ .
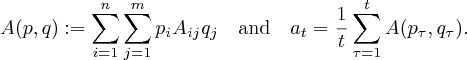
For each pair $(p,q)$ , there is a payoff vector $A(p,q)\in{\mathbb R}^k$ and average payoff vector $a_t\in{\mathbb R}^k$ . Here $\label{blackwell:A} A(p,q):=\sum_{i=1}^n\sum_{j=1}^m p_iA_{ij}q_j\quad\text{and}\quad a_t=\frac{1}{t}\sum_{\tau=1}^t A(p_\tau,q_\tau).$
At each time $t$ , we assume $p_t$ is chosen as a function of $A(\cdot,\cdot)$ and the past decisions $\{(p_\tau,q_\tau)\}_{\tau=1}^{t-1}$ .
We say that $\{a_\tau\}_{\tau=1}^\infty$ approaches a set ${\mathcal A}\subset {\mathbb R}^p$ if the distance between $a_t$ and ${\mathcal A}$ converges to zero, namely, $d(a_t,\mA):=\inf_{\alpha\in\mA} ||a_t-\alpha||_2 \xrightarrow[t\rightarrow\infty]{} 0.$

Theorem (Blackwell’s Approachability Theorem): For closed convex set ${\mathcal A}$ , the following are equivalent

${\mathcal A}$ is approachable.
For every $q$ there exists $p$ such that $A(p,q)\in {\mathcal A}$ .
Every half space containing ${\mathcal A}$ is approachable.¹

Before a proof we comment on how Blackwell’s Approachability Theorem relates to the Minimax Theorem.

For $A(p,q)\in {\mathbb R}$ , $\max_{q} \min_p A(p,q)=\min_p \max_{q} A(p,q)$ holds iff the following are equivalent for every $v\in {\mathbb R}$ i. $\exists p$ $\forall q$ s.t. $A(p,q)\leq v$ , $\:\:$ [“without knowing $q$ , we can think of a good $p$ ”]ii. $\forall q\; \exists p$ s.t. $A(p,q)\leq v$ .
[“if we know $q$ , we can think of a good $p$ ”]
Blackwell’s Approachability Theorem now makes the assumption that $A(p,q)$ is a vector.
The equivalence between (1) and (2) found in Blackwell’s Approachability Theorem is analogous to the equivalence between (i) and the seemingly weaker statement (ii) found in the Minimax Theorem.
However, we note that Approachability (1) is weaker than the statement $\exists p$ $\forall q$ s.t. $A(p,q)\in {\mathcal A}$ . Approachability states $\exists$ $\{p_t\}_{t=1}^\infty$ (chosen sequentially) so that $\forall$ $\{ q_t \}_{t=0}^\infty$ on average $A(p_t,q_t)$ converges to ${\mathcal A}$ as $t\rightarrow \infty$ .
Finally, we observe that (3) approaching a half-space ${\mathcal H}=\{a : n\cdot a \leq v\}$ corresponds to applying the Minimax Theorem to game matrix $\hat{A}$ whose $i,j$ -th component is $n\cdot A_{ij}$ .

Proof: $2\implies 3$ : For every ${\mathcal H} = \{a : n\cdot a \leq v\}$ containing ${\mathcal A}$ ,

$\begin{aligned} \forall q\; \exists p \text{ s.t. } A(p,q)\in\mA &\implies \forall q\; \exists p \text{ s.t. } n\cdot A(p,q) \leq v \underbrace{\implies}_{\substack{\text{Minimax}\\\text{Theorem}}} \exists p\; \forall q \text{ s.t. } n\cdot A(p,q) \leq v \underbrace{\implies}_{\substack{\text{choose}\\p_t=p\; \forall t}} \mH\text{ approachable}. \end{aligned}$

$3\implies 2$ : For every ${\mathcal H} = \{a : n\cdot a \leq v\}$ containing ${\mathcal A}$ ,

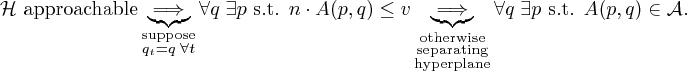
$\begin{aligned} \mH\text{ approachable} \underbrace{\implies}_{\substack{\text{suppose}\\q_t=q\; \forall t}} \forall q\; \exists p \text{ s.t. } n\cdot A(p,q) \leq v \underbrace{\implies}_{\substack{\text{otherwise}\\\text{separating}\\ \text{hyperplane}}} \forall q\; \exists p \text{ s.t. } A(p,q)\in\mA. \end{aligned}$

$1 \implies 3$ : $A\subset {\mathcal H}=\{a : n\cdot a \leq v\}$ so is immediate.

$3 \implies 1$ : Firstly note

$\begin{aligned} \label{blackwell equivi} \mH\text{ approachable} \underbrace{\implies}_{\substack{\text{suppose}\\q_t=q\; \forall t}} \forall q\; \exists p \text{ s.t. } n\cdot A(p,q) \leq v \underbrace{\implies}_{\substack{\text{Minimax}\\\text{Theorem}}} \exists p\; \forall q \text{ s.t. } n\cdot A(p,q) \leq v \end{aligned}$

At time $t$ , let the projection $P(a_t)$ be closest point to $a_t$ in ${\mathcal A}$ and let ${\mathcal H}_t$ be the half-space containing ${\mathcal A}$ defined by normal $n_t=P(a_t)-a_t$ and $v_t=P(a_t)\cdot (P(a_t)-a_t)$ . In other words, ${\mathcal H}_t$ is defined by the hyperplane through $P(a_t)$ perpendicular to $P(a_t)-a_t$ . Since ${\mathcal H}_t$ is approachable, we can see from there must exist a $p_t$ such that $A(p_t,q)\in {\mathcal H}_t$ for all distributions $q$ . Using this $p_t$ .

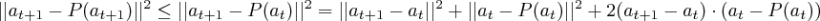
$\begin{aligned} \label{Blackwell:parallellogram} ||a_{t+1}- P(a_{t+1})||^2 &\leq || a_{t+1} - P(a_t)||^2 = || a_{t+1} -a_{t} ||^2 + || a_t - P(a_t) ||^2 +2 (a_{t+1}-a_t)\cdot (a_t-P(a_t)) \end{aligned}$

As $a_{t+1}=A(p_t,q_t)/(t+1) + ta_t/(t+1)$ , we now extract $A(p_{t+1},q_{t+1})-P(a_t)$ from the term $(a_{t+1}-a_t)\cdot (a_t-P(a_t))$ :

$\begin{aligned} (a_{t+1}-a_t)\cdot (a_t-P(a_t)) &= \frac{A(p_{t+1},q_{t+1})}{t+1}\cdot ( a_t-P(a_t)) - \frac{a_{t}}{t+1}\cdot (a_t-P(a_t)) \notag\\ &= \frac{1}{t+1}\Big[ (A(p_{t+1},q_{t+1}) - P(a_t) )\cdot ( a_t-P(a_t)) - ({a_{t}}-P(a_t)\cdot (a_t-P(a_t)) \Big] \label{Blackwell:sub} \end{aligned}$

Substituting this expression, we have

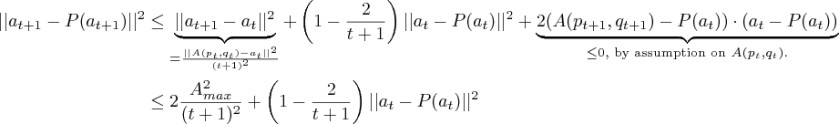
$\begin{aligned} ||a_{t+1}- P(a_{t+1})||^2 &\leq \underbrace{||a_{t+1}-a_{t}||^2}_{=\frac{|| A(p_t,q_t) -a_t ||^2}{(t+1)^2}} + \left( 1- \frac{2}{t+1} \right) || a_t - P(a_t) ||^2 +\underbrace{2 (A(p_{t+1},q_{t+1})-P(a_t) )\cdot (a_t-P(a_t))}_{ \leq 0,\text{ by assumption on }A(p_t,q_t).}\\ &\leq 2 \frac{A^2_{max}}{(t+1)^2} + \left( 1- \frac{2}{t+1} \right) || a_t - P(a_t) ||^2 \end{aligned}$

Thus multiplying both sides by $(t+1)^2$ and rearranging gives

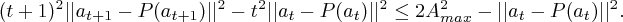
$(t+1)^2||a_{t+1}- P(a_{t+1})||^2 - t^2||a_{t}- P(a_{t})||^2 \leq 2 A^2_{max} - || a_t - P(a_t) ||^2.$

Summing these interpolating terms gives

$t^2 || a_t - P(a_t) ||^2 \leq 2A^2_{max} t - \sum_{\tau=0}^t || a_\tau - P(a_\tau) ||^2 \leq 2A^2_{max}t$

Thus, as required,

$\label{blackwell: conv} || a_t - P(a_t) || \leq A_{max}\sqrt{\frac{2}{t}}\xrightarrow[t\rightarrow\infty]{} 0.$

$\square$

(Typo: the term 2A_{\max}^2 in the last 4 displays above should be 4A_{\max}^2.)

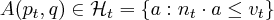Note that our proof is constructive. We define a policy for choosing $p_t$ such that $A(p_t,q) \in \mH_t= \{ a : n_t \cdot a \leq v_t\}$ where from $P(a_t)$ , the projection of $a_t$ onto ${\mathcal A}$ we define $n_t=P(a_t)-a_t$ and $v_t=P(a_t)\cdot (P(a_t)-a_t)$ .

We now consider one interesting consequence of this result.

Theorem (Hannan-Gaddum Theorem)

Suppose $A(p,q)$ as defined in is such that $A(p,q)\in {\mathcal A}$ . There exists a playing strategy $\{p_t\}_{t=1}^\infty$ such that for any $\{q_t\}_{t=1}^\infty$

$\label{blackwell:regret} \limsup_{t\rightarrow\infty}\left\{\frac{1}{t}\sum_{\tau=1}^t A(p_t,q_t) - \min_{i=1,...,m} \frac{1}{t}\sum_{\tau=1}^t A(i,q_t)\right\}\leq 0.$

In other words, our performance in the game is asymptotically as good as the best fixed action.

Proof:

We verify Blackwell’s Approachability Theorem for the vector payoff $\hat{A}(p,q)=(A(p,q)-A(i,q)\; :\; i=1,...,m)$ and convex region ${\mathcal A}=\{a: a_i\leq 0, i=1,...,m\}$ . For all $q$ there exists $p$ such that component-wise $\hat{A}(p,q)\leq 0$ , in particular we choose $p_{i^*}=1$ where $A(i^*,q)=\min_{i=1,...,m} A(i,q)$ . This verifies condition 2. of Blackwell’s Approachability Theorem. Thus there exists a strategy $\{p_t\}_{t=1}^\infty$ such that for all $\{q_t\}_{t=1}^\infty$

$\left\{\frac{1}{t}\sum_{\tau=1}^t A(p_t,q_t) - \frac{1}{t}\sum_{\tau=1}^t A(i,q_t)\right\} \vee 0 \xrightarrow[t\rightarrow\infty]{} 0$

which is equivalent to the required expression above.

Recall a half-space in ${\mathbb R}^k$ is a set ${\mathcal H}=\{a\in {\mathbb R}^k : n\cdot a \leq c\}$ for some $n\in {\mathbb R}^k$ and $c\in {\mathbb R}^k$ .↩

2 thoughts on “Blackwell Approachability”

Chen Chen says:

September 29, 2020 at 3:28 am

Excellent notes! One question: in the proof of the Blackwell’s Approachability Theorem, (3) -> (1): I wonder why ||A(p_t, q_t), a_t||^2 can be uniformly bounded from above by a constant 2A_{max}^2?

LikeLike

chenc11 says:

October 4, 2020 at 4:55 pm

Excellent notes! For the proof of the Blackwell’s Approachability Theorem, (3) to (1): Can I ask why ||A(p_t, q_t) – a_t||^2 can be uniformly bounded from above by a constant 2 A_{max}^2?

LikeLike

Share this:

Like this:

2 thoughts on “Blackwell Approachability”

Leave a Reply to Chen Chen Cancel reply