Kalman Filter

Kalman filtering (and filtering in general) considers the following setting: we have a sequence of states $x_t$ , which evolves under random perturbations over time. Unfortunately we cannot observe $x_t$ , we can only observe some noisy function of $x_t$ , namely, $y_t$ . Our task is to find the best estimate of $x_t$ given our observations of $y_t$ .

Consider the equations

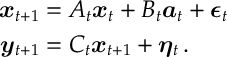
$\begin{aligned} \bm x_{t+1} &= A_t \bm x_t + B_t \bm a_t + \bm \epsilon_{t}\, \\ \bm y_{t+1} &= C_t\bm x_{t+1} + \bm \eta_t\, .\end{aligned}$

where $\epsilon_t \sim \mathcal N ( 0, \Sigma^\epsilon_t)$ , $\eta_t ) \sim \mathcal N ( 0, \Sigma^\eta_t)$ and $\epsilon_t$ and $\nu_t$ are independent. (We let $\Sigma^{\epsilon}$ be the sub-matrix of the covariance matrix corresponding to $\epsilon$ and so forth…)

The Kalman filter has two update stages: a prediction update and a measurement update. These are

Screenshot 2019-05-14 at 07.12.37.png and

where

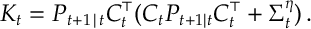
$\begin{aligned} K_t = P_{t+1\, |\, t} C^\top_t ( C_t P_{t+1|t} C_t^\top + \Sigma^\eta_t )\, .\end{aligned}$

The matrix $K_t$ is often referred to as the Kalman Gain. Assuming the initial state $x_0$ is known and deterministic $P_{0|0} =0$ in the above.

We will use the following proposition, which is a standard result on normally distributed random vectors, variances and covariances,

Prop 1. Let $u$ be normally distributed vector with mean $\bar{u}$ and covariance $\Sigma_{ u}$ , i.e.

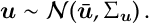
$\bm u \sim \mathcal N (\bar{\bm u}, \Sigma_{\bm u })\, .$

i) For any matrix $A$ and (constant) vector $c$ , we have that

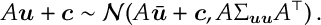
$A\bm u +\bm c \sim \mathcal N (A \bar{\bm u} + \bm c , A \Sigma_{\bm u \bm u} A^\top )\, .$

ii) If we take $u = ( v, w)$ then $w$ conditional on $v$ gives

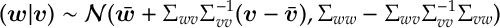
$(\bm w | \bm v) \sim \mathcal N (\bar{\bm w} + \Sigma_{w v} \Sigma^{-1}_{v v} (\bm v - \bar{\bm v}) ,\Sigma_{ww} - \Sigma_{w v} \Sigma^{-1}_{v v} \Sigma_{v w} )$

iii) $Var ( A u ) = A\Sigma_u A^\top$ , $Cov ( Au , Bu) = A \Sigma_u B^\top$ .

We can justify the Kalman filtering steps by proving that the conditional distribution of $x_{t+1}$ is given by the Prediction and measurement steps. Specifically we have the following.

Theorem 1.

$\begin{aligned} (\bm x_{t+1} | \bm y_{[0:t]}, \bm a_{[0:t]} ) & \sim \mathcal N ( \hat{\bm x}_{t+1|t } , P_{t+1|t} ) \\ (\bm x_{t+1} | \bm y_{[0:t+1]}, \bm a_{[0:t]} ) & \sim \mathcal N ( \hat{\bm x}_{t+1|t+1 } , P_{t+1|t+1} )\end{aligned}$

where $y_{[0:t]} := (y_0,...,y_{t})$ and $a_{[0:t]} := (a_0,...,a_{t})$ .

Proof. We show the result by induction supposing that

$(\bm x_{t} | \bm y_{[0:t]}, \bm a_{[0:t]} ) \sim \mathcal N ( \hat{\bm x}_{t|t } , P_{t|t} )\, .$

Since $x_{t+1}$ is a linear function of $x_t$ , we have that

$(\bm x_{t+1} | \bm y_{[0:t]}, \bm a_{[0:t]} ) \sim \mathcal N ( \hat{\bm x}_{t+1|t } , P_{t+1|t} )\, .$

where, by Prop 1ii), we have that

$\hat{\bm x}_{t+1} = A_t \hat{\bm x}_{t|t} + B_t a_t\, , \qquad P_{t+1|t} = A_t P_{t|t} A^\top_t + \Sigma^\epsilon_t\, .$

Given $y_{t+1} = C_t x_{t+1} + \eta_t$ , we have by Prop 1iii) that $Var(y_{t+1} | y_{[0,t]}, a_{[0,t]}) = C_t P_{t+1|t} C^\top_t$ and $Cov(x_{t+1}, y_{t+1} | y_{[0,t]}, a_{[0,t]}) = P_{t+1|t} C^\top_t$ . Thus

$\begin{aligned} ( [\bm x_{t+1} , \bm y_{t+1}] | \bm y_{[0:t]} , \bm a_{[0:t]} ) \sim \mathcal N \left( [ \hat{\bm x}_{t+1|t } , C_t \hat{\bm x}_{t+1|t } ] , \left[ \begin{array}{ll} P_{t+1|t} & P_{t+1} C^\top_t \\ C_t P_{t+1|t} & C_t P_{t+1} C_t^\top + \Sigma^\eta_t \end{array} \right) \right]\, .\end{aligned}$

Thus applying Prop 1ii), we get that

$\begin{aligned} (x_{t+1} | y_{[0:t+1]} , a_{[0:t]} ) & = ( (x_{t+1} | y_{[0:t]} , a_{[0:t]} ) | y_{t+1}) \\ & \sim \mathcal N \Big( \hat{\bm x}_{t+1|t} + P_{t+1 | t} C^\top_t [ C_t P_{t+1} C^\top_t + \Sigma^\eta_t ]^{-1} ( y_{t+1} - C_t \hat{\bm x}_{t+1|t} ) \, ,\\ & \qquad\qquad \qquad\quad P_{t+1|t} - P_{t+1|t} C^\top_t [ C_t P_{t+1|t} C_t^\top + \Sigma^\eta_t ]^{-1} C_t P_{t+1|t} \Big)\, . \end{aligned}$

$ \square$

Literature

The Kalman filter is generally credited to Kalman and Bucy. The method is now standard in many text books on control and machine learning.

Kalman, Rudolph E., and Richard S. Bucy. “New results in linear filtering and prediction theory.” (1961): 95-108.

Share this:

Leave a comment Cancel reply