Continuous Time Dynamic Programs

Continuous-time dynamic programs
The HJB equation; a heuristic derivation; and proof of optimality.

Discrete time Dynamic Programming was given in previously (see Dynamic Programming ). We now consider the continuous time analogue.

Time is continuous $t\in\mathbb{R}_+$ ; $x_t\in \mathcal{X}$ is the state at time $t$ ; $a_t\in \mathcal{A}$ is the action at time $t$ ;

Def 1 [Plant Equation] Given function $f: \mathbb{R}_+\times\mathcal{X}\times \mathcal{A}_t \rightarrow \mathcal{X}$ , the state evolves according to a differential equation

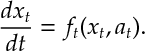
$\frac{dx_{t}}{dt}= f_t(x_t, a_t).$

This is called the Plant Equation.

Def 2 A policy $\pi$ chooses an action $\pi_t$ at each time $t$ . The (instantaneous) reward for taking action $a$ in state $x$ at time $t$ is $r_t(a,x)$ and $r_T(x)$ is the reward for terminating in state $x$ at time $T$ .

Def 3 [Continuous Dynamic Program] Given initial state $x_0$ , a dynamic program is the optimization

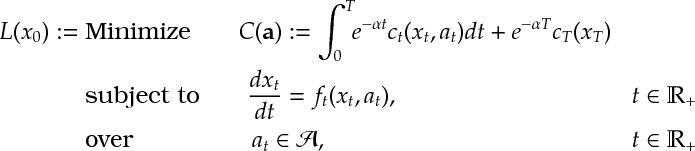
$\begin{aligned} L(x_0):=\; &\text{Minimize} \qquad C({\bf a}) := \int_{0}^{T}\!\! e^{-\alpha t}c_t(x_t,a_t) dt + e^{-\alpha T}c_T(x_T)\\ & \text{subject to} \qquad \frac{dx_{t}}{dt}= f_t(x_t, a_t), & t\in\mathbb{R}_+ \notag \\ & \text{over}\qquad \quad\qquad a_t \in \mathcal{A},& t\in\mathbb{R}_+\notag \end{aligned}$

Further, let $C_\tau({\bf a})$ (Resp. $L_\tau(x_\tau)$ ) be the objective (Resp. optimal objective) for when the summation is started from $t=\tau$ , rather than $t=0$ .

When a minimization problem where we minimize loss given the costs incurred is replaced with a maximization problem where we maximize winnings given the rewards received. The functions $L$ , $C$ and $c$ are replaced with notation $W$ , $R$ and $r$ .

Def 4 [Hamilton-Jacobi-Bellman Equation] For a continuous-time dynamic program , the equation

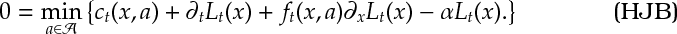
$\label{cDP:HJB}\tag{HJB} 0= \min_{a\in\mathcal{A}} \left\{ c_t(x,a)+ \partial_t L_t(x) + f_t(x,a)\partial_x L_t(x) - \alpha L_t(x). \right\}$

is called the Hamilton-Jacobi-Bellman equation. It is the continuous time analogoue of the Bellman equation [[DP:Bellman]].

Ex 1 [A Heuristic derivation of the HJB equation] Argue that, for $\delta>0$ small, $x$ satisfying the recursion

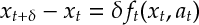
$\label{cDP:xaprox} x_{t+\delta} -x_{t} = \delta f_t(x_t,a_t)$

is a good approximation to the plant equation . (A heuristic argument will suffice)

Ex 2 [Continued] Argue (heuristically) that following is a good approximation for the objective of a continuous time dynamic program is

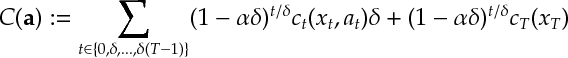
$\begin{aligned} \label{cDP:Ob} C({\bf a}) := \sum_{t\in\{0,\delta,...,\delta(T-1)\} } (1-\alpha \delta)^{ {t}/{\delta}}c_t(x_t,a_t) \delta + (1-\alpha \delta)^{ {t}/{\delta}}c_T(x_T) \end{aligned}$

Ex 3 [Continued]Show that the Bellman equation for the discrete time dynamic program with objective and plant equation is

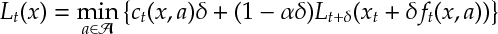
$L_t(x) = \min_{a\in \mathcal{A}}\left\{ c_t(x,a)\delta + (1-\alpha \delta) L_{t+\delta}(x_t+\delta f_t(x,a)) \right\}$

Ex 4 [Continued]Argue, by letting $\delta$ approach zero, that the above Bellman equation approaches the equation

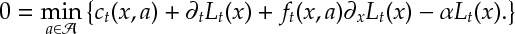
$0= \min_{a\in\mathcal{A}} \left\{ c_t(x,a)+ \partial_t L_t(x) + f_t(x,a)\partial_x L_t(x) - \alpha L_t(x). \right\}$

Ex 5 [Optimality of HJB]Suppose that a policy $\Pi$ has a value function $C_t(x,\Pi)$ that satisfies the HJB-equation for all $t$ and $x$ then, show that $\Pi$ is an optimal policy.

(Hint: consider $e^{-\alpha t}C_t(\tilde{x}_t,\Pi)$ where $\tilde{x}$ are the states another policy $\tilde{\Pi}$ .)

Answers

Ans 1 Obvious from definition of derivative.

Ans 2 Obvious from definition of (Riemann) Integral and since $(1-\alpha \delta)^{t/\delta}\rightarrow e^{-\alpha t}$ as $\delta\rightarrow 0$ .

Ans 3 Immediate from discrete time Bellman Equation.

Ans 4 Minus $L_t(x)$ from each side in [3] divide by $\delta$ and let $\delta\rightarrow 0$ . Further note that

$\frac{(1-\alpha \delta) L_{t+\delta}(x+\delta f) - L_t(x)}{\delta} \xrightarrow[\delta \rightarrow 0]{ }\partial_t L_t(x) + f_t(x,a)\partial_x L_t(x) - \alpha L_t(x).$

Ans 5 Using shorthand $C=C_t(\tilde{x}_t,\Pi)$ :

$\begin{aligned} -\frac{d}{dt} \left(e^{-\alpha t} C_t(\tilde{x}_t,\Pi)\right)&=e^{-\alpha t} \left\{ c_t(\tilde{x}_t,\tilde{\pi}_t) - \left[ c_t(\tilde{x}_t,\tilde{\pi}_t) - \alpha C + f_t(\tilde{x}_t,\tilde{\pi}_t) \partial_x C + \partial_t C\right]\right\}\\ &\leq e^{-\alpha t} c_t(\tilde{x}_t,\tilde{\pi}_t) \end{aligned}$

The inequality holds since the term in the square brackets is the objective of the HJB equation, which is not maximized by $\tilde{\pi}_t$ .

Answers

Share this:

Leave a comment Cancel reply