Markov’s Inequality; Chebychev’s Inequality; Chernoff’s Bound.
Bounds for the Poisson Distribution.

Throughout this section we assume that $X$ is a real valued random variable. The mean, variance and moment generating function of $X$ are, respectively, $\mu$ , $\sigma$ and $M_X(\theta)$ , when these exist.

Ex 1. [Markov’s Inequality] For positive random variable $X$

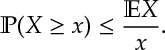
$\mathbb{P} ( X \geq x ) \leq \frac{\mathbb{E} X}{x}.$

Markov’s inequality can be thought of as an upper-bound on the probability or as a lower-bound on the expectation:

Ex 2. Let $m$ be the mode of $X$ , i.e. ${\mathbb P}( X\leq m) = \frac{1}{2}$ then

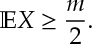
$\bE X\geq \frac{m}{2} .$

(Similar logic applies to other quartiles.)

Ex 3. [Chebychev’s Inequality] For $X$ with mean $\mu$ and variance $\sigma$

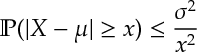
$\mathbb{P}( |X-\mu| \geq x ) \leq \frac{\sigma^2}{x^2}$

Ex 4. For a positive increasing function $f$ ,

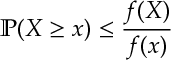
$\mathbb{P} ( X \geq x ) \leq \frac{f(X)}{f(x)}$

Ex 5. [Chernoff’s Bound]

$\mathbb{P} ( X \geq x ) \leq \exp\Big\{- \min_{\theta\geq 0} \big( \theta x - \log M_X(\theta)\big)\Big\}$

Let’s get some handy exponential and normal tail bounds for the Poisson distribution.

Ex 6. [Some Poisson Bounds] For $Po(\mu)$ , a Poisson random variable with parameter $\mu$ ,

$\mathbb{E} [e^{\theta Po(\mu)}] = e^{\mu (e^{\theta} -1)}$

and

$\min_{\theta} \left\{e^{-\theta x} \bE [e^{\theta Po(\mu)}]\right\} = \exp \left\{ - \mu \left[ \left( 1- \frac{x}{\mu}\right)+ \frac{x}{\mu}\log\frac{x}{\mu}\right] \right\}$

Ex 7. [Continued]

$\begin{aligned} &{\mathbb P} \left( Po(\mu) \geq x \right) \leq e^{-\mu-x },\qquad \forall x\geq \mu e^2\\ &{\mathbb P} \left( Po(\mu) \leq x \right) \leq e^{-\mu+x },\qquad \forall x\in [0,\mu]. \end{aligned}$

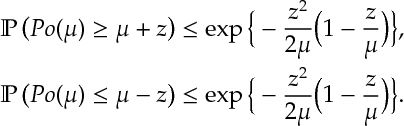
Ex 8.[Continued] For $z\geq 0$ , $\begin{aligned} &{\mathbb P} \left( Po(\mu) \geq \mu +z \right) \leq \exp\big\{-\frac{z^2}{2\mu}\big(1-\frac{z}{\mu}\big)\big\},\\ &{\mathbb P} \left( Po(\mu) \leq \mu -z \right) \leq \exp\big\{-\frac{z^2}{2\mu}\big(1-\frac{z}{\mu}\big)\big\}. \end{aligned}$

Answers.

Ans 1. $\mathbb{I} [X \geq x] \leq \frac{X}{x}$ now take expectations.

Ans 2. Applying Markov’s inequality

$\bE [X] \geq m (1- \bP(X\leq m)) = \frac{m}{2}.$

Ans 3. Consider $|X-\mu| \geq x$ , square both sides and apply Markov [1].

Ans 4. Consider $X \geq x$ , apply $f$ to both sides and then [1].

Ans 5. Take $f(x)=e^{\theta x}$ apply [4], then minimize over theta.

Ans 6. First equality is straightforward. Second, $\frac{d}{d\theta} (\mu e^\theta -\theta x)=0$ implies $\theta= \log \left(\frac{x}{\mu} \right)$ which after substitution gives the bound.

Ans 7. First bound: The Chernoff bound [5] gives

$\mathbb{P} \left(Po(\mu) \geq x \right) \leq \exp \left\{ - \mu \left[ \left( 1- \frac{x}{\mu}\right)+ \frac{x}{\mu}\log\frac{x}{\mu}\right] \right\}$

By assumption $\log \frac{x}{\mu}\geq 2$ , substituting this into the logorithm above gives the result. Second, by the same Chernoff bound and use that $\frac{x}{\mu}\log \frac{x}{\mu} \leq 0$ .