Robbins-Munro

We review the proof by Robbins and Munro for finding fixed points. Stochastic gradient descent, Q-learning and a bunch of other stochastic algorithms can be seen as variants of this basic algorithm. We review the basic ingredients of the original proof.

Often it is important to find a solution to the equation

by evaluating $g$ at a sequence of points. For instance Newton’s method would perform the updates $x_{n+1} = x_n - g(x_n)/g'(x_n)$ . However, Robbins and Munro consider the setting where we cannot directly observe $g$ but we might observe some random variable whose mean is $g(x)$ . Thus we observe

$\label{RM:Regress} y_n = g(x_n) + \epsilon_n$

and hope solve for $g(x) = 0$ . Notice in this setting, even if we can find $g'(x)$ , Newton’s method may not converge. The key idea of Robbins and Munro is to use a schema

$\label{RM:RM} x_{n+1} = x_n - \alpha_n y_n \tag{RM}$

where we chose the sequence $\{\alpha_n\}_{n=0}^\infty$ so that

$\sum_{n} \alpha_n = \infty, \qquad \sum_{n} \alpha_n^2 < \infty\, .$

Before proceeding here are a few different use cases:

Quartiles. We want to find $x$ such that $P(X \leq x ) = p$ for some fixed $p$ . But we can only sample the random variable $X$ .
Regression. We preform regression $g(x) = \beta_0 + \beta_1 x$ , but rather than estimate $\beta$ we want to know where $g(x)=0$ .
Optimization. We want to optimize a convex function $f(x)$ whose gradient is $g(x)$ . Assume that $f(x) = \sum_{k=1}^K f_k(x)$ for some large $K$ . To find the optimum at $g(x)=0$ we randomly sample (uniformly) $f_k(x)$ whose gradient, $g_k(x)$ , is an bias estimate of $g(x)$ .

Robbins-Munro Proof.

We now go through the main steps of Robbins and Munro’s proof. This proof is intentionally not the most general but instead gives the key ideas.

We assume that $g(x)$ is an increasing, smooth, real-valued function from $[x_{\min},x_{\max}]$ to $[y_{\min},y_{\max}]$ and that there is a unique point $x^*$ such that $g(x^*)=0$ . Further assume $g'(x^*) \neq 0$ and that samples $y_n= g(x_n)+\epsilon_n$ belong to the interval $[y_{\min},y_{\max}]$ and $\mathbb E [\epsilon_n] = 0$ .

In the steps below we prove the following:

Thrm [Robbins-Munro] If we chose $x_n$ acording to the Robbin-Munro step rule then we have that

$\mathbb E [ (x_n - x^* ) ^2 ] \xrightarrow[]{n\rightarrow} 0$

where here $x^*$ satisfies $g(x^*)=0$ .

Ex 1. Let $b_n = \mathbb E [ (x_n-x^*)^2]$ . Show that for Robbins-Munro

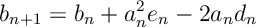
$b_{n+1} = b_n + a_n^2 e_n - 2 a_n d_n\,$

for terms

Ans 1.

$\begin{aligned} b_{n+1} & = \mathbb E ( x_{n+1} - x_n + x_n - x^*)^2 \\ &= \mathbb E ( x_{n+1} - x_n )^2 + 2\mathbb E [(x_{n+1} - x_n ) ( x_n - x^* )] + \mathbb E ( x_n - x^*)^2 \\ & = \alpha^2_n \mathbb E [ y_n^2] - 2 \alpha_n \mathbb E [g(x_n) ( x_n - x^* )] + \mathbb E ( x_n - x^*)^2 \\ & = a_n^2 e_n - 2 a_n d_n + b_n \end{aligned}$

as required.

Ex 2. Argue that $d_n \geq \kappa b_n$ for some constant $\kappa > 0$ .

Ans 2. Since $g(x)$ is increasing, smooth and $g'(x^*)>0$ it must be that

$\frac{g(x) - g(x^*)}{x- x^*} > \kappa , \qquad \text{for all } x\in [x_{\min},x_{\max}]\, .$

Thus

$d_n = \mathbb E [ ( x_n - x^* ) ( g(x_n) - g(x^*) ) ] \geq \kappa \mathbb E [ ( x_n - x^* ) (x_n - x^* ) ] = \kappa b_n \, .$

Ex 3. Argue that if $\sum_n \alpha^2_n <\infty$ then $\sum_n \alpha_n d_n < \infty$ and $\lim_{n\rightarrow\infty} b_n$ exists.

Ans 3. Summing the expression for [[RM:1]] over $n$ gives

$- b_0 \leq \lim_{n\rightarrow \infty} ( b_n - b_0 ) = \sum_{n=0}^\infty (b_{n+1} - b_{n}) = \sum_n a^2_n e_n - 2\sum_n a_n d_n \, .$

Since $e_n$ is bounded and $\sum_n a^2_n$ is finite it must be that $\sum_n \alpha_n d_n < \infty$ and $\lim_{n\rightarrow\infty} b_n$ exists.

Ex 4. Finally argue that if $\sum_n a_n = \infty$ then

$b_n = \mathbb E [ (x_n - x^*)^2 ] \xrightarrow[n\rightarrow \infty]{} 0 \, .$

Ans 4. We know from [3] and [3] that

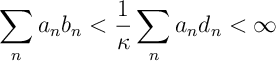
$\sum_n a_n b_n < \frac{1}{\kappa} \sum_n a_n d_n < \infty$

Since we choose $\{ a_n\}$ so that $\sum_n a_n = \infty$ . It must be that $\liminf_{n\rightarrow \infty} b_n = 0$ . Further since we know the limit $\lim_{n\rightarrow \infty} b_n$ exists it must be that $\lim_{n\rightarrow \infty} b_n = 0$ , as required.