Merton Portfolio Optimization

We consider a specific diffusion control problem. We focus on setting where there is one risky asset and one riskless asset, though we will see that much of the analysis passes over to multiple assets.

Def. [The Merton Problem – Plant Equation] In the Merton problem you wish to optimise your long run consumption. You may invest your wealth in a bank account receiving riskless interest $r$ , or in a risky asset with value $S_t$ obeying the following SDE

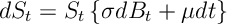
$dS_t = S_t \left\{ \sigma dB_t + \mu dt \right\}$

where each $B=(B_t:t\geq 0)$ is an independent standard Brownian motion.

Wealth $(W_t : t\geq 0)$ obeys the SDE

$\begin{aligned} d W_t &= r\underbrace{ (W_t - n_t S_t ) }_{ \substack{\text{\tiny{Wealth in}}\\ \text{\tiny{bank}}} } dt \; + \; \underbrace{ n_t dS_t }_{ \substack{\text{\tiny{Wealth in}}\\ \text{\tiny{asset}}} } - \underbrace{ c_t dt }_{ \text{\tiny{consumption}} } \\ &= r \left(W_t - n_t\cdot S_t\right) dt + n_t \cdot dS_t - c_t dt \end{aligned}$

You can control $c_t$ your rate of consumption at time $t$ and $n_t$ the number of stocks the risky asset at time $t$ . Also, we define $\theta_t = n_t S_t$ to be the wealth in the risky asset at time $t$ .

Def. [The Merton Problem – Objective] Given the above plant equation, , the objective is to maximize the long-term utility of consumption

$\begin{aligned} V(w_0) = \max_{(n_t,c_t)_{t\geq 0}\mathcal P ( w_0)} \mathbb{E}\left[\int_0^\infty e^{-\rho t} u(c_t) dt\right]. \end{aligned}$

Here $\rho$ is a positive constant and $u(c)$ is a concave increasing utility function. The set $\mathcal P(w_0)$ is the set of policies given initial wealth $w_0$ . Further, let $V(w,t)$ be the optimal objective with the integral starting for time $t$ with $w_t=w$ .

Let’s write the wealth respect to integrals in $dt$ and $dB_t$ :

Ex 1. Show that

$dW_t = e^{-\rho t} \partial _w V(W_t) \left[ r \left(W_t - n_t\cdot S_t\right) dt + n_t \cdot dS_t - c_t dt \right]$

Ans 1.

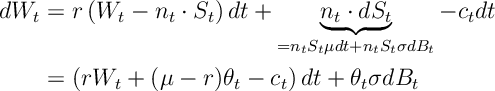
$\begin{aligned} dW_t & = r \left(W_t - n_t\cdot S_t\right) dt + \underbrace{n_t \cdot dS_t}_{= n_t S_t \mu dt + n_t S_t \sigma dB_t} - c_t dt \\ & = \left( rW_t + (\mu -r ) \theta_t - c_t \right) dt + \theta_t \sigma dB_t \end{aligned}$

Ex 2. Show that

$V(w,t) = e^{-\rho t} V(x).$

Ans 2. Notice if we shift time by $\tau$ , a factor $e^{-\rho t}$ comes out,

$V(w,\tau) = \max_{(n_t,c_t)_{t\geq \tau}} \mathbb{E}\left[\int_\tau^\infty e^{-\rho t} u(c_t) dt\right] = \max_{(n_t,c_t)_{t\geq 0}} \mathbb{E}\left[\int_0^\infty e^{-\rho (t+\tau)} u(c_t) dt\right] = e^{-\rho \tau}V(w)\, .$

Ex 3. Show that the HJB equation for the Merton Problem can be written as

$0 = \max_{c} \left\{ u(c) - c \partial_w V \right\} + \max_{\theta }\left\{ \theta (\mu -r ) + \frac{1}{2}\sigma^2 \theta^2\partial_{ww} V \right\} -\rho V + r w \partial_w V$ or, alternatively, as

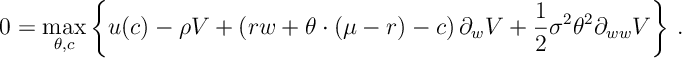
$\begin{aligned} 0 & = \max_{\theta, c }\left\{ u(c) -\rho V + \left( rw + \theta \cdot (\mu-r)-c \right) \partial_w V + \frac{1}{2}\sigma^2 \theta^2\partial_{ww} V\right\}\, .\end{aligned}$

Ans 3. Recall that informally the HJB equation is

$0=\max_{\text{actions}} \left\{ \text{$

Notice that if we apply Ito’s formula to $V(W_t)$ we get that

$\begin{aligned} d V ( W_t ) & = \partial _w V(W_t ) dW_t +\partial_t V(W_t ) dt + \frac{1}{2} \partial_{ww} V(W_t) d [W]_t \\ & = \partial _w V(W_t) \left[ r \left(W_t - n_t\cdot S_t\right) dt + n_t \cdot dS_t - c_t dt \right] \\ & + \partial_t V(W_t) dt + \frac{\theta^2\sigma^2}{2} \partial_{ww} V(W_t) dt\end{aligned}$

Applying this to the above term gives as required

$\begin{aligned} 0 & = \max_{\theta, c }\left\{ u(c) -\rho V + \left( rw + \theta \cdot (\mu-r)-c \right) \partial_w V + \frac{1}{2}\sigma^2 \theta^2\partial_{ww} V\right\}\\ & = \max_{c} \left\{ u(c) - c \partial_w V \right\} + \max_{\theta }\left\{ \theta (\mu -r ) + \frac{1}{2}\sigma^2 \theta^2\partial_{ww} V \right\} -\rho V + r w \partial_w V\end{aligned}$

Ex 4. [Continued] Optimizing the HJB over $\theta$ , show that

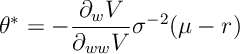
$\theta^* = - \frac{\partial_{w} V }{\partial_{ww} V} \sigma^{-2} (\mu-r)$

Ans 4. Differentiating the HJB equation in [[cDP:MertonHJB]] wrt $\theta$ gives

$\sigma^2 \theta \partial_{ww} V = - (\mu -r) \partial_w V.$

Now rearrange for $\theta^*$ .

Ex 5. [Continued] Given $\theta^*$ , show that the HJB equation becomes

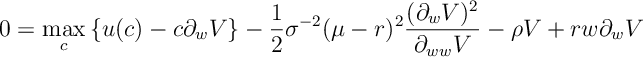
$0 = \max_{c} \left\{ u(c) - c \partial_w V \right\} - \frac{1}{2} \sigma^{-2} (\mu - r)^2 \frac{(\partial_w V)^2}{\partial_{ww} V} -\rho V + r w \partial_w V$

Ans 5. Substituting gives

$\max_{\theta }\left\{ \theta (\mu -r ) + \frac{1}{2}\sigma^2 \theta^2\partial_{ww} V \right\} = \theta^* ( \mu - r ) + \frac{1}{2} \sigma^2 \theta^{*2}\partial_{ww} V = - \frac{1}{2} \sigma^{-2} (\mu - r)^2 \frac{(\partial_w V)^2}{\partial_{ww} V}$

Merton for CRRA Utility

We focus on the case of CRRA utility, that is:

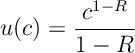
$u(c)= \frac{c^{1-R}}{1-R}$

for $R >0$ (Recall the discussion on utility functions, Section [Util]). Thus we wish to solve for

$\begin{aligned} V(w_0) = \max_{(n_t,c_t)_{t\geq 0}} \mathbb{E}\left[\int_0^\infty e^{-\rho t} \frac{c_t^{1-R}}{1-R} dt\right]. \end{aligned}$

Ex 6. Show that

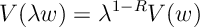
$V(\lambda w)= \lambda^{1-R}V(w)$

Ans 6. Here we note that having a policy for initial wealth $\lambda w_0$ is the same as having a policy of wealth $w_0$ and then multiplying each amount invested by $\lambda$ :

$\begin{aligned} V(\lambda w) & = \max_{(n_t,c_t)_{t\geq 0}\in \mathcal P (\lambda w_0)} \mathbb{E}\left[ \int_0^\infty e^{-\rho t} \frac{c_t^{1-R}}{1-R} dt \right] \\ & = \max_{(n_t,c_t)_{t\geq 0}\in \mathcal P ( w_0)} \mathbb{E}\left[ \int_0^\infty e^{-\rho t} \frac{ (\lambda c_t)^{1-R}}{1-R} dt \right] = \lambda^{1-R} V(w). \end{aligned}$

Ex 7. Show that

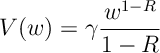
$V(w)= \gamma \frac{w^{1-R}}{1-R}$

for some position constant $\gamma >0$ .

Ans 7. In [6], let $\lambda=w^{-1}$ and $\gamma = (1-R)V(1)$ .

Ex 8. Show that

$\partial_w V(w) = \gamma w^{-R} \quad \text{and} \quad \partial_{ww} V(w) = -R \gamma w^{-xR-1}$

Ans 8. Trival.

Ex 9. Show that if we define

$\tilde{u}(z) = \sup_c \left\{ u(c) - c z \right\}$

then for a CARA utility

$\tilde{u}(z) = - \frac{ y^{1-R^{-1}} }{ 1-R^{-1} }.$

Ans 9. Differentiating gives $c^{-R} = z$ now rearrange and substitute.

Ex 10. Show that, when optimizing over $c$ , the HJB equation is optimized by

$c^*= \gamma^{-\frac{1}{R}}w.$

Ans 10.

$\begin{aligned} \sup_{c} \left\{ u(c) - c \partial_w V \right\} \implies u'(c) = \partial_w V = \gamma w^{-R}\end{aligned}$

which since $u'(c)=c^{-R}$ , gives the required formed.

Ex 11. [Merton:CARA4] Show that

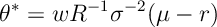
$\theta^* = wR^{-1} \sigma^{-2} (\mu-r)$

Ex 12. [Continued]Show that

$\sup_{c} \left\{ u(c) - c \partial_w V \right\} = \frac{R}{1-R} \gamma^{1-\frac{1}{R}} w^{1-R}$

Ans 12. By [8] and [10]

$\begin{aligned} \sup_{c} \left\{ u(c) - c \partial_w V \right\} & = \frac{c^{*1-R}}{1-R} - c^* \partial_w V(c^*) \\ & = \frac{(\gamma^{-\frac{1}{R}}w)^{1-R}}{1-R} -(\gamma^{-\frac{1}{R}}w) \gamma w^{-R} \\ & = \frac{R}{1-R} \gamma^{1-\frac{1}{R}} w^{1-R}\end{aligned}$

Ex 13. Given the optimal choices of $c$ and $\theta$ , Show that the HJB equation to be satisfied it must be that

$\gamma^* = R^{-1} \left\{ \rho + (R-1) \left( r+ \frac{1}{2} \frac{\kappa^2}{R} \right) \right\}$

where

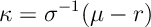
$\kappa = \sigma^{-1} (\mu-r)$

To summarize: we notice we have show that the parameters given by

$\theta^* = \frac{w}{R} \sigma^{-2} (\mu-r)\, , \quad c^*= \gamma^{-\frac{1}{R}}w\, , \quad \gamma^* = R^{-1} \left\{ \rho + (R-1) \left( r+ \frac{1}{2} \frac{\kappa^2}{R} \right) \right\}$

in exercises [4, 10, 13] give a solution to the HJB equation for the Merton problem. (Although we have not yet proven them to be optimal.)

We now give rigourous argument for the optimality of parameters $c^*$ , $\theta^*$ and $\gamma^*$ for the Merton problem with CRRA utility. (This section can be skipped if preferred.)

Ex 14. Show that

$\mathbb{E} \left[ \int_{0}^{\infty} e^{-\rho t } u(c_t) dt \right] - \mathbb{E} \left[ \int_{0}^{\infty} e^{-\rho t } u(c^*_t) dt \right] \leq \mathbb E \left[ \int_{0}^{\infty} \left( c_t-c^*_t \right) \zeta_t dt \right]$ where

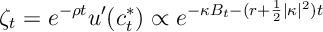
$\zeta_t = e^{-\rho t} u'(c^*_t) \propto e^{-\kappa B_t -(r+\frac{1}{2} |\kappa|^2)t}$

(Hint: $u(y)$ is concave.)

Ans 14. Since $u(y)$ is concave we have that $u(y) \leq u(x) + (y-x) u'(x)$ . Thus

$\begin{aligned} \mathbb E \left[ \int_0^\infty e^{-\rho t} u(c_t) dt \right] & \leq \mathbb E \left[ \int_0^\infty e^{-\rho t} \left\{ u(c^*_t) + (c_t - c^*_t ) u'(c^*_t) \right\} dt \right]\\ & = \mathbb E \left[ \int_0^\infty e^{-\rho t} u(c^*_t) dt \right] + \mathbb E \left[ \int_{0}^{\infty} \left( c_t-c^*_t \right) \zeta_t dt \right]\end{aligned}$

Ex 15. Verify that

$Y_t = \zeta_t W_t + \int_{0}^{t} \zeta_s c_s ds$

is a positive local martingale. [Hint: apply Ito’s formula to

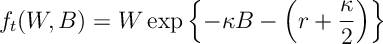
$f_t( W, B) = W \exp \left\{ - \kappa B - \Big(r + \frac{\kappa}{2} \Big) \right\}$

]

Ex 16. [Continued] Show that

$w_0 \geq \mathbb{E} \left[ \int_{0}^{\infty} \zeta_s c_s ds \right]$

[Hint: Doob’s Martingale Convergence Theorem.]

Ans 16. Recall from stochastic integration theory that every positive local martingale is a supermartingale. Doob’s Martingale Convergence Theorem applied to [15] gives

$w_0 = Y_0 \geq \mathbb E Y_{\infty} = \mathbb E \left[ \int_0^\infty \zeta_s c_s ds \right]$

Ex 17. [Continued] By direct calculation show that

$w_0 = \mathbb{E} \left[ \int_{0}^{\infty} \zeta_s c_s^* ds \right]$

[Hint: apply Fubini’s Theorem and note that

$\mathbb E \left[ e^{\alpha B_t - \frac{\alpha^2}{2} t} \right]=1$

]

Ex 18. Now show that

$\mathbb{E} \left[ \int_{0}^{\infty} e^{-\rho t } u(c_t) dt \right] \leq \mathbb{E} \left[ \int_{0}^{\infty} e^{-\rho t } u(c^*_t) dt \right]$

Ans 18. Combining [16] and [17], we see that $\mathbb E \left[ \int_{0}^{\infty} \left( c_t-c^*_t \right) \zeta_t dt \right] \leq 0\, .$

Applying this to [14] we see that

$\mathbb{E} \left[ \int_{0}^{\infty} e^{-\rho t } u(c_t) dt \right] \leq \mathbb{E} \left[ \int_{0}^{\infty} e^{-\rho t } u(c^*_t) dt \right]$

as required. Thus $c^*_t$ is optimal.

The last exercise shows that the portfolio $\theta^*,c^*$ is optimal for the Merton problem with CRRA utility.

One thought on “Merton Portfolio Optimization”

Pingback: More on Merton Portfolio Optimization – Applied Probability Notes

Merton for CRRA Utility

Share this:

Like this:

One thought on “Merton Portfolio Optimization”

Leave a Reply Cancel reply