We review the proof by Robbins and Munro for finding fixed points. Stochastic gradient descent, Q-learning and a bunch of other stochastic algorithms can be seen as variants of this basic algorithm. We review the basic ingredients of the original proof.
Often it is important to find a solution to the equation

by evaluating at a sequence of points. For instance Newton’s method would perform the updates
. However, Robbins and Munro consider the setting where we cannot directly observe
but we might observe some random variable whose mean is
. Thus we observe

and hope solve for . Notice in this setting, even if we can find
, Newton’s method may not converge. The key idea of Robbins and Munro is to use a schema

where we chose the sequence so that

Before proceeding here are a few different use cases:
- Quartiles. We want to find
such that
for some fixed
. But we can only sample the random variable
.
- Regression. We preform regression
, but rather than estimate
we want to know where
.
- Optimization. We want to optimize a convex function
whose gradient is
. Assume that
for some large
. To find the optimum at
we randomly sample (uniformly)
whose gradient,
, is an bias estimate of
.
Robbins-Munro Proof.
We now go through the main steps of Robbins and Munro’s proof. This proof is intentionally not the most general but instead gives the key ideas.
We assume that is an increasing, smooth, real-valued function from
to
and that there is a unique point
such that
. Further assume
and that samples
belong to the interval
and
.
In the steps below we prove the following:
Thrm [Robbins-Munro] If we chose acording to the Robbin-Munro step rule then we have that
![\mathbb E [ (x_n - x^* ) ^2 ] \xrightarrow[]{n\rightarrow} 0](https://appliedprobability.blog/wp-content/uploads/2018/09/19df2650bca37a40b7b4fc05a21288fc.png?w=840)
where here satisfies
.
Ex 1. Let . Show that for Robbins-Munro
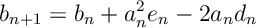
for terms

Ans 1.
![\begin{aligned} b_{n+1} & = \mathbb E ( x_{n+1} - x_n + x_n - x^*)^2 \\ &= \mathbb E ( x_{n+1} - x_n )^2 + 2\mathbb E [(x_{n+1} - x_n ) ( x_n - x^* )] + \mathbb E ( x_n - x^*)^2 \\ & = \alpha^2_n \mathbb E [ y_n^2] - 2 \alpha_n \mathbb E [g(x_n) ( x_n - x^* )] + \mathbb E ( x_n - x^*)^2 \\ & = a_n^2 e_n - 2 a_n d_n + b_n \end{aligned}](https://appliedprobability.blog/wp-content/uploads/2018/09/00a7ca0dcf7e9f81b5440a4701cd5c3c.png?w=840)
as required.
Ex 2. Argue that for some constant
.
Ans 2. Since is increasing, smooth and
it must be that
![\frac{g(x) - g(x^*)}{x- x^*} > \kappa , \qquad \text{for all } x\in [x_{\min},x_{\max}]\, .](https://appliedprobability.blog/wp-content/uploads/2018/09/be78273f5e021f1e4d6aacd5c6582b19.png?w=840)
Thus
![d_n = \mathbb E [ ( x_n - x^* ) ( g(x_n) - g(x^*) ) ] \geq \kappa \mathbb E [ ( x_n - x^* ) (x_n - x^* ) ] = \kappa b_n \, .](https://appliedprobability.blog/wp-content/uploads/2018/09/5dc47fa16ba827c2ed681ae2167c1b83.png?w=840)
Ex 3. Argue that if then
and
exists.
Ans 3. Summing the expression for [[RM:1]] over gives

Since is bounded and
is finite it must be that
and
exists.
Ex 4. Finally argue that if then
![b_n = \mathbb E [ (x_n - x^*)^2 ] \xrightarrow[n\rightarrow \infty]{} 0 \, .](https://appliedprobability.blog/wp-content/uploads/2018/09/69cb1e2f0ea2610c714ad804a764448a.png?w=840)
Ans 4. We know from [3] and [3] that
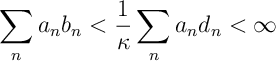
Since we choose so that
. It must be that
. Further since we know the limit
exists it must be that
, as required.